
分析 根据等式的变化可找出变化规律“$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$”,依此规律即可得出结论.
解答 解:观察,发现规律:$\frac{1}{1×2}$=1-$\frac{1}{2}$,$\frac{1}{2×3}$=$\frac{1}{2}-\frac{1}{3}$,$\frac{1}{3×4}$=$\frac{1}{3}$-$\frac{1}{4}$,…,
∴$\frac{1}{5×6}$=$\frac{1}{5}$-$\frac{1}{6}$,$\frac{1}{n(n+1)}$=$\frac{1}{n}$-$\frac{1}{n+1}$,
∴$\frac{1}{1×2}$+$\frac{1}{2×3}$+$\frac{1}{3×4}$+…+$\frac{1}{99×100}$=1-$\frac{1}{2}$+$\frac{1}{2}$-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{4}$+…+$\frac{1}{99}$-$\frac{1}{100}$=1-$\frac{1}{100}$=$\frac{99}{100}$.
故答案为:$\frac{1}{5}$-$\frac{1}{6}$;$\frac{1}{n}$-$\frac{1}{n+1}$.
点评 本题考查了规律型中数字的变化类,根据数的变化找出变化规律是解题的关键.


 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
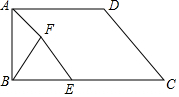 如图所示,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=7,BC=10,CD=6,E是BC边上一动点,以BE为一边在BC上方作等边△BEF,联结AF.
如图所示,已知梯形ABCD中,AD∥BC,∠ABC=90°,AD=7,BC=10,CD=6,E是BC边上一动点,以BE为一边在BC上方作等边△BEF,联结AF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
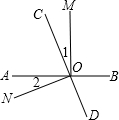 如图,直线AB、CD相交于点O,OM⊥AB.
如图,直线AB、CD相交于点O,OM⊥AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com