
在△ABC中,∠A=90°,AB=4,AC=3,M是AB上的动点(不与A、B重合),过M作MN//BC交AC于点N,以MN为直径作⊙O,设AM=x

(1)用含x的代数式表示△AMN的面积S;
(2)M在AB上运动,当⊙O与BC相切时(如图①),求x的值;
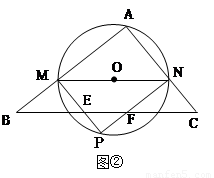
(3)M在AB上运动,当⊙O与BC相交时(如图②),在⊙O上取一点P,使PM//AC,连接PN,PM交BC于E,PN交BC于点F,设梯形MNFE的面积为y,求y关于x的函数关系式。
(1) (2)
(2)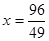 (3)
(3)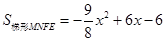
【解析】
试题分析:27、解:(1)∵MN//BC,∴∠AMN=∠B,∠ANM=∠C
∴△AMN∽△ABC
∴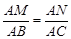 ,即
,即 ,∴
,∴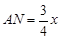
∵AM⊥AN,∴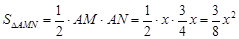
(2)设BC与⊙O相切于点D,连接AO、OD,

则AO=OD=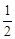 MN
MN
在Rt△ABC中,
又∵△AMN∽△ABC,
∴ ,即
,即 ,∴
,∴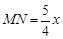 ,∴
,∴
过M作MQ⊥BC于Q,则
则△BMQ∽△ABC,
∴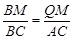 ,∴
,∴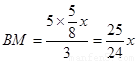
∵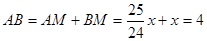
∴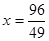
(3)
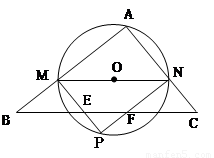
∵∠A=90°,PM//AC,∠MPN=90°
∴四边形AMPN是矩形
∴PN=AM=x
又∵四边形BFNM是平行四边形,
∴FN=BM=8-x,PF=PN-FN=x-(4-x)=2x-4
又Rt△PEF∽Rt△ABC,∴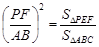 ,
,
∴
∵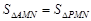
∴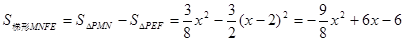
考点:动点问题
点评:本题难度较大,主要考查学生结合四边形性质和相似三角形性质等知识点解决动点问题的综合能力,为中考常考题型,要求学生多做训练,掌握这类题型解题技巧。确定动点在一定范围内的函数关系式为解题关键。


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com