
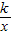 (k>0)的图象与边交于点E.
(k>0)的图象与边交于点E.
 ,
, ;
; ,
, ,
,
 -
- -
-
 .
. ,
, ,
, ,k2=6(不合,舍去).
,k2=6(不合,舍去). 时,S=
时,S= =
=


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| k | x |
 存在,求出点F的坐标;若不存在,请说明理由.
存在,求出点F的坐标;若不存在,请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:
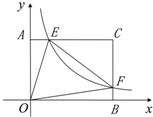 面直角坐标系.若点F是边BC上的一个动点(不与B、C重合),过F点的反比例函数y=
面直角坐标系.若点F是边BC上的一个动点(不与B、C重合),过F点的反比例函数y=| k | x |
查看答案和解析>>
科目:初中数学 来源: 题型:
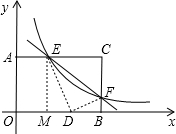 已知:在矩形AOBC中,OB=4,OA=3.分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数y=
已知:在矩形AOBC中,OB=4,OA=3.分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系.F是边BC上的一个动点(不与B,C重合),过F点的反比例函数y=| k |
| x |
| ED |
| DF |
查看答案和解析>>
科目:初中数学 来源:2010-2011学年河南油田中招第二次模拟考试数学试卷(解析版) 题型:解答题
已知:在矩形AOBC中,OB=4,OA=3,分别以OB、OA所在直线为x轴和y轴,建立如图所示的平面直角坐标系,F是边BC上的一个动点(不与B、C重合),过F点的反比例函数 (k>0)的图象与AC边交于点E.
(k>0)的图象与AC边交于点E.
(1)求证:△AOE与△BOF的面积相等.
(2)记S=S△OEF-S△ECF,求当k为何值时,S有最大值,最大值为多少?
(3)请探索:是否存在这样的点F,使得将△CEF沿EF对折后,C点恰好落在OB上?若存在,请直接写出点F的坐标,若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com