




 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:2012届浙江省四校九年级联考数学卷(带解析) 题型:解答题
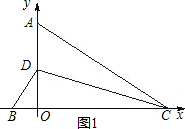
阅读材料:如图1:直线 ,点A,B,C,D分别在
,点A,B,C,D分别在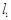 和
和 上,因为“两平行线间的距离处处相等”,所以
上,因为“两平行线间的距离处处相等”,所以 ,
, .
.
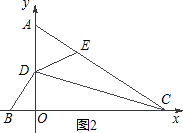
解决问题:如图2:在梯形ABCD中,AB∥CD,AC,BD相交于点O,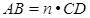 (n>1的正实数),梯形ABCD的面积为S.请回答下列问题:
(n>1的正实数),梯形ABCD的面积为S.请回答下列问题:
(1)请直接写出相应的值:①当n=2时,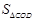 = ▲ S;②当n=3时,
= ▲ S;②当n=3时,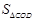 = ▲ S;
= ▲ S;
③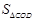 = ▲ S(用n的代数式表示);
= ▲ S(用n的代数式表示);
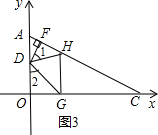
(2)如图3,点E,F分别在AD,BC的中点, EF分别交AC,BD于M,N,,求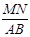 的值(用n的代数式表示);
的值(用n的代数式表示);
(3)在(2)中,根据上面的结论,当 时,直接写出n的值.
时,直接写出n的值.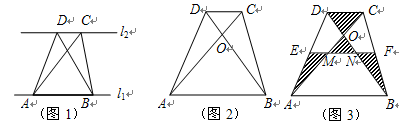
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com