
·ЦОц КЧПИёщѕЭКэµДїЄ·ЅµДФЛЛг·Ѕ·ЁЈ¬·Ц±рЗуіц$\sqrt{{4}^{2}+{3}^{2}}$Ўў$\sqrt{{44}^{2}+{33}^{2}}$Ўў$\sqrt{{444}^{2}+{333}^{2}}$Ўў$\sqrt{{4444}^{2}+{3333}^{2}}$µДЦµёчКЗ¶аЙЩЈ»И»єуёщѕЭЛщµГµДЅб№ыЧЬЅбіц№жВЙЈ¬ІўДЬУ¦УГЧЬЅбµД№жВЙЈ¬ІВПл$\sqrt{\underset{\underbrace{44Ў{4}^{2}}}{2015ёц}+\underset{\underbrace{33Ў{3}^{2}}}{2015ёц}}$µДЅб№ыОЄ¶аЙЩјґїЙЈ®
Ѕвґр ЅвЈєёщѕЭ·ЦОцЈ¬їЙµГ
ЈЁ1Ј©$\sqrt{{4}^{2}+{3}^{2}}$=5Ј»
ЈЁ2Ј©$\sqrt{{44}^{2}+{33}^{2}}$=55Ј»
ЈЁ3Ј©$\sqrt{{444}^{2}+{333}^{2}}$=555Ј»
ЈЁ4Ј©$\sqrt{{4444}^{2}+{3333}^{2}}$=5555Ј»
ІВПл$\sqrt{\underset{\underbrace{44Ў{4}^{2}}}{2015ёц}+\underset{\underbrace{33Ў{3}^{2}}}{2015ёц}}$µДЅб№ыОЄЈє$\underset{\underbrace{55Ў5}}{2015ёц5}$Ј®
№Кґр°ёОЄЈє5Ўў55Ўў555Ўў5555Ўў$\underset{\underbrace{55Ў5}}{2015ёц5}$Ј®
µгЖА ґЛМвЦчТЄїјІйБЛјЖЛгЖч-КэµДїЄ·ЅОКМвЈ¬ТФј°МЅС°№жВЙОКМвµДУ¦УГЈ¬ТЄКмБ·ХЖОХЈ¬ЧўТв№ЫІмЧЬЅбіц№жВЙЈ¬ІўДЬХэИ·µДУ¦УГ№жВЙЈ®



| Дкј¶ | ёЯЦРїОіМ | Дкј¶ | іхЦРїОіМ |
| ёЯТ» | ёЯТ»Гв·СїОіМНЖјцЈЎ | іхТ» | іхТ»Гв·СїОіМНЖјцЈЎ |
| ёЯ¶ю | ёЯ¶юГв·СїОіМНЖјцЈЎ | іх¶ю | іх¶юГв·СїОіМНЖјцЈЎ |
| ёЯИэ | ёЯИэГв·СїОіМНЖјцЈЎ | іхИэ | іхИэГв·СїОіМНЖјцЈЎ |
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєСЎФсМв
| AЈ® | -2 | BЈ® | 0 | CЈ® | -$\frac{5}{2}$ | DЈ® | 2 |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєМоїХМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєСЎФсМв
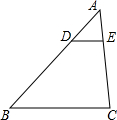 ИзНјЈ¬ФЪЎчABCЦРЈ¬DEЎОBCЈ¬$\frac{AD}{DB}=\frac{1}{2}$Ј¬ФтПВБРЅбВЫЦРХэИ·µДКЗЈЁЎЎЎЎЈ©
ИзНјЈ¬ФЪЎчABCЦРЈ¬DEЎОBCЈ¬$\frac{AD}{DB}=\frac{1}{2}$Ј¬ФтПВБРЅбВЫЦРХэИ·µДКЗЈЁЎЎЎЎЈ©| AЈ® | $\frac{AE}{EC}=\frac{1}{2}$ | BЈ® | $\frac{DE}{BC}=\frac{1}{2}$ | ||
| CЈ® | $\frac{ЎчADEµДЦЬі¤}{ЎчABCµДЦЬі¤}=\frac{1}{2}$ | DЈ® | $\frac{ЎчADEµДГж»э}{ЎчABCµДГж»э}=\frac{1}{3}$ |
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєМоїХМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєЅвґрМв
Ійїґґр°ёєНЅвОц>>
їЖДїЈєіхЦРКэС§ АґФґЈє МвРНЈєМоїХМв
Ійїґґр°ёєНЅвОц>>
№ъјКѧУУЕСЎ - Б·П°ІбБР±н - КФМвБР±н
єю±±КЎ»ҐБЄНшОҐ·ЁєНІ»БјРЕПўѕЩ±ЁЖЅМЁ | НшЙПУРє¦РЕПўѕЩ±ЁЧЁЗш | µзРЕХ©ЖѕЩ±ЁЧЁЗш | ЙжАъК·РйОЮЦчТеУРє¦РЕПўѕЩ±ЁЧЁЗш | ЙжЖуЗЦИЁѕЩ±ЁЧЁЗш
ОҐ·ЁєНІ»БјРЕПўѕЩ±Ёµз»°Јє027-86699610 ѕЩ±ЁУКПдЈє58377363@163.com