计算:．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

5．计算：（3x+9）（6x-8）．

分析根据多项式乘以多项式法则即可求出答案．

解答解：原式=18x²-24x+54x-72=18x²+30x-72；

点评本题考查多项式乘以多项式法则，属于基础题型．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

16．求下列各式的值：
（1）sin30°•sin²45°-$\frac{tan45°-tan60°}{sin30°}$；
（2）$\sqrt{ta{n}^{2}30°-2tan30°+1}$+|tan60°-1|；
（3）2^-1+（π-3.14）⁰+sin60°-|-$\frac{\sqrt{3}}{2}$|

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

16．在关于x的方程2ax-1=0（a≠0）中，把a叫做字母系数．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．

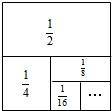利用图形来表示数量或数量关系，也可以利用数量或数量关系来描述图形特征或图形之间的关系，这种思想方法称为数形结合．我们刚学过的第9章《整式乘法与因式分解》就很好地体现了这一思想方法，你能利用数形结合的思想解决下列问题吗？
（1）如图，一个边长为1的正方形，依次取正方形面积的$\frac{1}{2}$、$\frac{1}{4}$、$\frac{1}{8}…$$\frac{1}{2^n}$，根据图示我们可以知道：$\frac{1}{2}$+$\frac{1}{4}$+$\frac{1}{8}$+$\frac{1}{16}$+…+$\frac{1}{2^n}$=1-$\frac{1}{{2}^{n}}$．
（2）利用上述公式计算：
①2-2²-2³-2⁴-2⁵-2⁶-…-2²⁰⁰⁸+2²⁰⁰⁹=6．
②计算：$\frac{2}{3}$+$\frac{2}{9}$+$\frac{2}{27}$+…+$\frac{2}{3^n}$=1-$\frac{1}{{3}^{n}}$．
③计算：$\frac{1}{3}$+$\frac{2}{9}$+$\frac{4}{27}$+…+$\frac{{{2^{n-1}}}}{3^n}$=1-$\frac{{2}^{n}}{{3}^{n}}$．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

20．直径为20cm的圆中，有一条长为10cm的弦，则这条弦所对的圆心角的度数是60°．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

10．阅读材料：解方程（x²-1）²-5（x²-1）+4=0，我们可以将x²-1视为一个整体，然后设x²-l=y，则（x²-1）²=y²，原方程化为y²-5y+4=0．①
解得y₁=1，y₂=4
当y=1时，x²-1=1．∴x²=2．∴x=±$\sqrt{2}$；
当y=4时，x²-1=4，∴x²=5，∴x=±$\sqrt{5}$．
∴原方程的解为x₁=$\sqrt{2}$，x₂=-$\sqrt{2}$，x₃=$\sqrt{5}$，x₄=-$\sqrt{5}$．
根据上面的解答，解决下面的问题：
（1）填空：在由原方程得到方程①的过程中，利用换元法达到了降次的目的，体现了换元的数学思想．
（2）解方程：x⁴-x²-12=0．

查看答案和解析>>

科目：初中数学 来源： 题型：填空题

17．若代数式$\sqrt{x+4}$有意义，则实数x的取值范围是x≥-4．

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

14．

有理数a、b在数轴上对应的位置如图所示，则（　　）

A．

a-b＜0

B．

a+b＞0

C．

a-b=0

D．

a-b＞0

查看答案和解析>>

科目：初中数学 来源： 题型：选择题

15．下列运算正确的是（　　）

	A．	a³+a³=3a⁶		B．	（-a）³•（-a）⁵=-a⁸
	C．	（-2a²b）•4a=-24a⁶b³		D．	（-$\frac{1}{3}$a-4b）（$\frac{1}{3}$a-4b）=16b²-$\frac{1}{9}$a²

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学