
(2010四川乐山)在△ABC中,D为BC的中点,O为AD的中点,直线l过点O.过A、B、C三点分别做直线l的垂线,垂足分别是G、E、F,设AG=h1,BE=h2,CF=h3.
(1)如图(12.1),当直线l⊥AD时(此时点G与点O重合).求证:h2+h3= 2h1;
(2)将直线l绕点O旋转,使得l与AD不垂直.
①如图(12.2),当点B、C在直线l的同侧时,猜想(1)中的结论是否成立,请说明你的理由;
②如图(12.3),当点B、C在直线l的异侧时,猜想h1、h2、h3满足什么关系.(只需写出关系,不要求说明理由)
![]()
![]()
(1)证明:∵BE⊥l,GF⊥l,
∴四边形BCFE是梯形.
又∵GD⊥l,D是BC的中点,
∴DG是梯形的中位线,
∴BE+CF=2DG.
又O为AD的中点,∴AG=DG,
∴BE+CF=2AG.
即h2+h3= 2h1.
(2)成立.
证明:过点D作DH⊥l,垂足为H,
∴∠AGO=∠DHO=Rt∠,∠AOG=∠DOH,OA=OD,
∴△AGO≌△DHO,
∴DH=AG.
又∵D为BC的中点,由梯形的中位线性质,
得2 DH=BE+CF,即2 AG =BE+CF,
∴h2+h3= 2h1成立.
(3)h1、h2、h3满足关系:h2-h3= 2h1.
(说明:(3)问中,只要是正确的等价关系都得分)


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
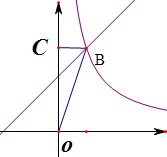
(2010四川乐山)如图(8)一次函数![]() 与反比例函数
与反比例函数![]() 在第一象限的图象交于点B,且点B的横坐标为1,过点B作y轴的垂线,C为垂足,若
在第一象限的图象交于点B,且点B的横坐标为1,过点B作y轴的垂线,C为垂足,若![]() ,
,
求一次函数和反比例函数的解析式
.
查看答案和解析>>
科目:初中数学 来源: 题型:
(2010四川乐山)如图(13.1),抛物线y=x2+bx+c与x轴交于A,B两点,与y轴交于点C(0,2),连接AC,若tan∠OAC=2.
(1)求抛物线对应的二次函数的解析式;
(2)在抛物线的对称轴l上是否存在点P,使∠APC=90°,若存在,求出点P的坐标;若不存在,请说明理由;
(3)如图(13.2)所示,连接BC,M是线段BC上(不与B、C重合)的一个动点,过点M作直线l′∥l,交抛物线于点N,连接CN、BN,设点M的横坐标为t.当t为何值时,△BCN的面积最大?最大面积为多少?O4YR%I2UNRAMG.jpg)

查看答案和解析>>
科目:初中数学 来源: 题型:
(2010四川乐山)某校对八年级(1)班全体学生的体育作测试,测试成绩分为优秀、良好、合格和不合格四个等级,根据测试成绩绘制的不完整统计图如下:
八年级(1)班体育成绩频数分布表 八年级(1)班体育成绩扇形统计图
| 等级 | 分值 | 频数 |
| 优秀 | 90—100分 | ? |
| 良好 | 75—89分 | 13 |
| 合格 | 60—74分 | ? |
| 不合格 | 0—59分9 |
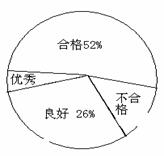
根据统计图表给出的信息,解答下列问题:
(1) 八年级(1)班共有多少名学生?
(2) 填空:体育成绩为优秀的频数是 ,为合格的频数是 ;
(3) 从该班全体学生的体育成绩中,随机抽取一个同学的成绩,求达到合格以上(包含合格)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com