
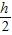 ;且BD=BF;进而可用h表示出BD,BF的长,再根据Rt△BEF∽Rt△BDC,可得
;且BD=BF;进而可用h表示出BD,BF的长,再根据Rt△BEF∽Rt△BDC,可得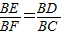 ;代入h的关系与BC=a可得答案;
;代入h的关系与BC=a可得答案;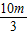 ;结合(1)的结论,可得a,h的值,进而可得CD的长,再根据三角函数的定义,可得答案.
;结合(1)的结论,可得a,h的值,进而可得CD的长,再根据三角函数的定义,可得答案.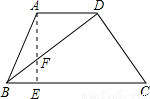 解:(1)根据题意,AD∥BC,且AF=EF;
解:(1)根据题意,AD∥BC,且AF=EF;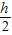 ;
;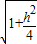 ;又可得AD=2AF;
;又可得AD=2AF;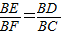 ;
;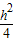 );即a=2+
);即a=2+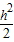 .
.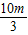 ;
;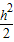 ;解可得a=20,h=6;
;解可得a=20,h=6;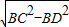 =16;
=16;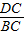 =
= .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:1998年全国中考数学试题汇编《二次函数》(01)(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:1998年浙江省绍兴市中考数学试卷 题型:解答题

查看答案和解析>>
科目:初中数学 来源:1998年浙江省绍兴市中考数学试卷 题型:解答题

查看答案和解析>>
科目:初中数学 来源:1998年浙江省绍兴市中考数学试卷 题型:选择题
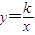 上有两点A(x1,y1)、B(x2,y2),若x2<x1<0,则y1与y2的大小关系是( )
上有两点A(x1,y1)、B(x2,y2),若x2<x1<0,则y1与y2的大小关系是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com