证明:(1)
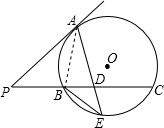
连接AB,
∵BE
2=DE•EA,
∴

=

,
∵∠E=∠E,
∴△DEB∽△BEA,
∴∠DBE=∠EAB,
∵PA切⊙O于A,
∴∠PAB=∠E,
∴∠PAB+∠BAE=∠E+∠DBE,
即∠PAD=∠ADP,
∴PA=PD;
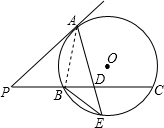
(2)证明:∵PA=PD,PA是⊙O的切线,PBC是⊙O的割线,
∴由切割弦定理得:PA
2=PB×PC=PD
2,
∵D为PC中点,
∴PD=DC,
∴PD
2=PB×2PD,
∴PD=2PB,DC=PD=2PB,
∵PD=PB+BD,
∴BD=PB,
由相交弦定理得:AD×DE=BD×DC,
∴AD×DE=PB×2PB,
即2PB
2=AD×DE.
分析:(1)连接AB,根据已知证△DEB∽△BEA,推出∠DBE=∠EAB,根据切线得出∠PAB=∠E,推出∠PAD=∠PDA即可;
(2)根据切割线定理和相交弦定理得出PA
2=PB×PC=PD
2,AD×DE=BD×DC,推出PB=BD=

PD=

DC,即可得出答案.
点评:本题考查了三角形外角性质,切线的性质,切割线定理,相交弦定理,相似三角形的性质和判定等知识点的综合运用,综合性比较强,有一定的难度.

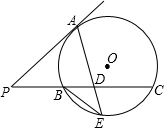 如图,PA切⊙O于A,割线PBC交⊙O于B、C两点,D为PC的中点,连AD并延长交⊙O于E,已知:BE2=DE•EA.求证:
如图,PA切⊙O于A,割线PBC交⊙O于B、C两点,D为PC的中点,连AD并延长交⊙O于E,已知:BE2=DE•EA.求证:
 =
= ,
,
 PD=
PD= DC,即可得出答案.
DC,即可得出答案.

 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案