Question

为美化青岛，创建文明城市，园林部门决定利用现有的3600盆甲种花卉和2900盆乙种花卉搭配、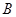两种园艺造型共50个，摆放在迎宾大道两侧．搭配每个造型所需花卉情况如右表所示：

结合上述信息，解答下列问题：

（1）符合题意的搭配方案有哪几种?

（2）若搭配一个种造型的成本为1000元，搭配一个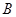种造型的成本为1200元，试说明选用（1）中哪种方案成本最低？

 

Answer 1

【答案】

（1）符合题意的搭配方案有3种，分别为：

第一种方案：种造型3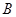0个，种20个；

第二种方案：种造型31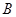个，种19个；

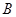第三种方案：种造型3２个，种18个；

（2）第三种方案成本最低。

【解析】

试题分析：设需要搭配x个A种造型，则需要搭配B种造型（50-x）个，根据“3600盆甲种花卉”“2900盆乙种花卉”列不等式求解，取整数值即可．通过计算可知第一种方案成本最低．

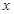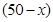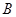（1）设需要搭配个种造型，则需要搭配个种造型．

由题意得：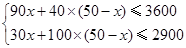

解得：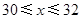

其正整数解为：，，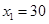

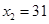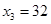
符合题意的搭配方案有3种，分别为：

第一种方案：种造型3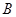0个，种20个；

第二种方案：种造型31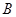个，种19个；

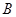第三种方案：种造型3２个，种18个．

（2）由题意知：三种方案的成本分别为：

第一种方案：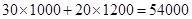

第二种方案：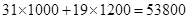

第三种方案：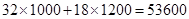

第三种方案成本最低

考点：本题考查的是一元一次不等式组的应用

点评：解决本题的关键是读懂题意，找到符合题意的不等关系式组．准确的解不等式组是需要掌握的基本能力．