从3,4,5这三个数中任取两个,分别记作p和q(p≠q),构造函数y=px-2和y=x+q,使这两个函数图象交点的横坐标始终小于2,则这样的有序数组(p,q)共有________对.
3
分析:分类讨论:把p=3,q=4;p=4,q=3;p=3,q=5;p=5,q=3;p=4,q=5;p=5,q=4时分别代入y=px-2和y=x+q,组成方程组,然后解方程组得到交点坐标,然后进行判断.
解答:当p=3,q=4时,解方程组
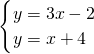
得
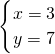
,即两直线的交点坐标为(3,7);
当p=4,q=3时,解方程组
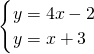
得
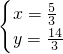
,即两直线的交点坐标为(

,

);
当p=3,q=5时,解方程组
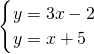
得
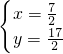
,即两直线的交点坐标为(

,

);
当p=5,q=3时,解方程组
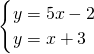
得
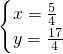
,即两直线的交点坐标为(

,

);
当p=4,q=5时,解方程组
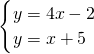
得
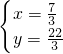
,即两直线的交点坐标为(

,
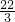
);
当p=5,q=4时,解方程组
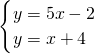
得
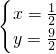
,即两直线的交点坐标为(

,

);
所以构造函数y=px-2和y=x+q,使这两个函数图象交点的横坐标始终小于2有(4,3)、(5,4)、(5,3).
故答案为3.
点评:本题考查了两直线平行或相交的问题:直线y=k
1x+b
1(k
1≠0)和直线y=k
2x+b
2(k
2≠0)平行,则k
1=k
2;若直线y=k
1x+b
1(k
1≠0)和直线y=k
2x+b
2(k
2≠0)相交,则交点坐标满足两函数的解析式.

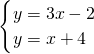 得
得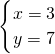 ,即两直线的交点坐标为(3,7);
,即两直线的交点坐标为(3,7);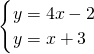 得
得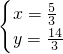 ,即两直线的交点坐标为(
,即两直线的交点坐标为( ,
, );
);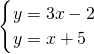 得
得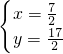 ,即两直线的交点坐标为(
,即两直线的交点坐标为( ,
, );
);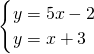 得
得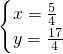 ,即两直线的交点坐标为(
,即两直线的交点坐标为( ,
, );
);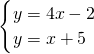 得
得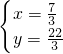 ,即两直线的交点坐标为(
,即两直线的交点坐标为( ,
,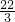 );
);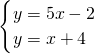 得
得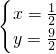 ,即两直线的交点坐标为(
,即两直线的交点坐标为( ,
, );
);

 名校课堂系列答案
名校课堂系列答案