
已知:直线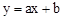 过抛物线
过抛物线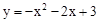 的顶点P,如图所示.
的顶点P,如图所示.
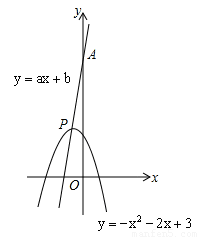
(1)顶点P的坐标是 ;
(2)若直线y=ax+b经过另一点A(0,11),求出该直线的表达式;
(3)在(2)的条件下,若有一条直线y=mx+n与直线y=ax+b关于x轴成轴对称,求直线y=mx+n与抛物线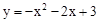 的交点坐标.
的交点坐标.
解:(1)∵y=﹣x2﹣2x+3=﹣(x 2+2x)+3=﹣(x+1) 2+4,
∴P点坐标为:(﹣1,4)。
(2)将点P(﹣1,4),A(0,11)代入y=ax+b得: ,解得:
,解得: 。
。
∴该直线的表达式为:y=7x+11。
(3)∵直线y=mx+n与直线y=7x+11关于x轴成轴对称,
∴y=mx+n过点P′(﹣1,﹣4),A′(0,﹣11)。
∴ ,解得:
,解得: 。
。
∴y=﹣7x﹣11。∴﹣7x﹣11=﹣x 2﹣2x+3。
解得:x1=7,x2=﹣2,此时y1=﹣60,y2=3。
∴直线y=mx+n与抛物线y=﹣x2﹣2x+3的交点坐标为:(7,﹣60),(﹣2,3)。
【解析】
试题分析:(1)利用配方法求出图象的顶点坐标即可:
(2)利用待定系数法求一次函数解析式即可。
(3)根据关于x轴对称点的坐标性质,首先求出直线y=mx+n的解析式,进而得出直线y=mx+n与抛物线y=﹣x2﹣2x+3的交点坐标。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
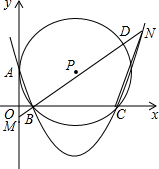 于A点,过A、B、C三点的⊙P与y轴相切于点A.M为y轴负半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N.
于A点,过A、B、C三点的⊙P与y轴相切于点A.M为y轴负半轴上的一个动点,直线MB交⊙P于点D,交抛物线于点N.查看答案和解析>>
科目:初中数学 来源: 题型:
| k |
| x |
| k |
| x |
查看答案和解析>>
科目:初中数学 来源:新课程 新理念 新思维·同步练习篇·数学 九年级下册(苏教版) 苏教版 题型:044
已知一直线过点P(3,-5),且与抛物线y=x2-3x-4有唯一交点,求这条直线的解析式.
查看答案和解析>>
科目:初中数学 来源:同步题 题型:解答题
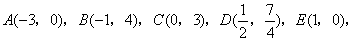
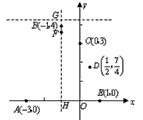
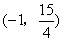 在抛物线的对称轴上,直线
在抛物线的对称轴上,直线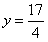 过点
过点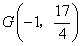 且垂直于对称轴。验证:以E(1,0)为圆心,EF为半径的圆与直线
且垂直于对称轴。验证:以E(1,0)为圆心,EF为半径的圆与直线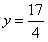 相切。请你进一步验证,以抛物线上的点
相切。请你进一步验证,以抛物线上的点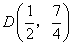 为圆心DF为半径的圆也与直线
为圆心DF为半径的圆也与直线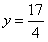 相切。由此你能猜想到怎样的结论。
相切。由此你能猜想到怎样的结论。 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com