
如图①,②,在平面直角坐标系 中,点
中,点 的坐标为(4,0),以点
的坐标为(4,0),以点![]() 为圆心,
为圆心,
4为半径的圆与 轴交于
轴交于 ,
, 两点,
两点, 为弦,
为弦, ,
, 是
是 轴上的一动点,连结
轴上的一动点,连结 .
.

(1)求![]() 的度数;(2分)
的度数;(2分)
(2)如图①,当 与⊙A相切时,求
与⊙A相切时,求![]() 的长;(2分)
的长;(2分)
(3)如图②,当点 在直径
在直径 上时,
上时, 的延长线与⊙A相交于点
的延长线与⊙A相交于点![]() ,问
,问![]() 为何值时,
为何值时,![]() 是等腰三角形?(5分)
是等腰三角形?(5分)
解:(1)∵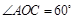 ,
,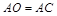 ,
,
∴![]() 是等边三角形. ∴
是等边三角形. ∴ .
.
(2)∵CP与⊙A相切,∴![]() .
.
∴![]() . ……………3分
. ……………3分
又∵![]() (4,0),∴
(4,0),∴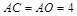 .∴
.∴![]() .
.
∴![]() . ………4分
. ………4分
(3)①过点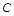 作
作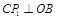 ,垂足为
,垂足为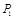 ,延长
,延长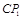 交⊙A于
交⊙A于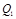 ,
,
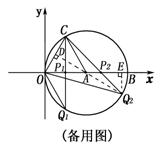
∵![]() 是半径, ∴CP1=Q1P1, ∴
是半径, ∴CP1=Q1P1, ∴![]() ,
,
∴![]() 是等腰三角形.…………………………5分
是等腰三角形.…………………………5分
又∵ 是等边三角形,∴
是等边三角形,∴![]() =2 .……6分
=2 .……6分
②解法一:过![]() 作
作![]() ,垂足为
,垂足为![]() ,延长
,延长![]() 交⊙A于
交⊙A于![]() ,
,![]() 与
与![]() 轴
轴
交于![]() ,∵
,∵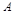 是圆心, ∴
是圆心, ∴ 是
是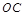 的垂直平分线. ∴
的垂直平分线. ∴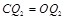 .
.
∴![]() 是等腰三角形, ………………………………7分
是等腰三角形, ………………………………7分
过点![]() 作
作![]() 轴于
轴于![]() ,在
,在![]() 中,
中,
∵![]() ,
,
∴![]() .∴点
.∴点 的坐标(4+
的坐标(4+![]() ,
, ).
).
在![]() 中,∵
中,∵ ,
,
∴![]() .∴
.∴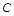 点坐标(2,
点坐标(2,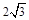 ).…………………8分
).…………………8分
设直线![]() 的关系式为:
的关系式为:![]() ,则有:
,则有:![]()
解得:![]() ∴
∴![]() .
.
当![]() 时,
时,![]() . ∴
. ∴![]()
解法二:过A作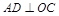 ,垂足为
,垂足为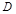 ,延长
,延长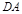 交⊙A于
交⊙A于 ,
,
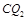 与
与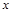 轴交于
轴交于 ,∵
,∵![]() 是圆心,
是圆心,
∴![]() 是
是![]() 的垂直平分线. ∴
的垂直平分线. ∴![]() .∴
.∴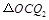 是等腰三角形.
是等腰三角形.
∵![]() ,∴
,∴ .
.
∵![]() 平分
平分![]() ,∴
,∴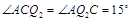 .
.
∵![]() 是等边三角形,
是等边三角形,![]() , ∴
, ∴![]() .
.
∴![]() .
.
∴![]() 是等腰直角三角形.∴
是等腰直角三角形.∴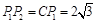 .
.
∴![]() .
.
解析:略


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案科目:初中数学 来源: 题型:
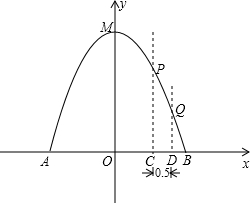 的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.
的体积和圆柱形桶的厚度忽略不计),以M点为顶点,抛物线对称轴为y轴,水平地面为x轴建立平面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:
 水柱在与池中心的水平距离为1m处达到最高,高度为3m.
水柱在与池中心的水平距离为1m处达到最高,高度为3m.查看答案和解析>>
科目:初中数学 来源: 题型:

| 多面体 | 面数a | 展开图的顶点数b | 展开图的棱数c |
| 直三棱柱 | 5 | 10 | 14 |
| 四棱锥 | 5 5 |
8 | 12 |
| 立方体 | 6 6 |
14 14 |
19 19 |
查看答案和解析>>
科目:初中数学 来源:学习周报 数学 华师大八年级版 2009-2010学年 第13期 总第169期 华师大版 题型:044
工具阅读:
在平面上画两条原点重合、互相垂直且具有相同单位长度的数轴(如图),这就建立了平面直角坐标系.通常把其中水平的一条数轴叫做x轴或横轴,取向右为正方向;铅直的数轴叫做y轴或纵轴,取向上为正方向;两数轴的交点O叫做坐标原点.

问题探究:如图1,在6×6的方格纸中,给出如下三种变换:P变换,Q变换,R变换.

将图形F沿x轴向右平移1格得图形F1,称为作1次P变换;
将图形F沿y轴翻折得图形F2,称为作1次Q变换;
将图形F绕坐标原点顺时针旋转90°得图形F3,称为作1次R变换.
规定:PQ变换表示先作1次Q变换,再作1次P变换;QP变换表示先作1次P变换,再作1次Q变换;Rn变换表示作n次R变换.
解答下列问题:
(1)作R4变换相当于至少作________次Q变换;
(2)请在图2中画出图形F作R2011变换后得到的图形F4;

(3)PQ变换与QP变换是否是相同的变换?请在图3中画出PQ变换后得到的图形F5,在图4中画出QP变换后得到的图形F6.

查看答案和解析>>
科目:初中数学 来源:2011-2012学年重庆市南开中学九年级(上)第一次月考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com