
分析 (1)根据有理数混合运算法则即可求出答案.
(2)根据乘法分配律即可求出答案.
(3)根据乘法分配律即可求出答案.
(4)根据整式加减的法则即可求出答案.
解答 解:(1)原式=16÷(-8)-$\frac{1}{2}$=-2-$\frac{1}{2}$=-2$\frac{1}{2}$
(2)原式=$\frac{1}{4}$×60-$\frac{1}{5}×60$+$\frac{1}{3}×60$=15-12+20=23
(3)原式=(999+$\frac{24}{25}$)×(-5)
=(999+1+$\frac{24}{25}$-1)×(-5)
=(1000-$\frac{1}{25}$)×(-5)
=-5000+$\frac{1}{5}$
=-$\frac{24999}{5}$
(4)原式=5a2b-10ab2+5c-8c-12a2b+4ab2
=-7a2b-6ab2-3c.
点评 本题考查学生的计算能力,解题的关键是熟练运用运算法则,本题属于基础题型.


科目:初中数学 来源: 题型:选择题
| A. | y=x2-2 | B. | y=x2+2 | C. | y=(x-2)2 | D. | y=(x+2)2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知AB是⊙O的直径,C、D为⊙O上两点,CG⊥AB于点F,CE⊥AD的延长线于点E,且CE=CF.
如图,已知AB是⊙O的直径,C、D为⊙O上两点,CG⊥AB于点F,CE⊥AD的延长线于点E,且CE=CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一根起点为0的数轴,现有同学将它弯折,弯折后虚线上第一行的数是0,第二行的数是6,第三行的数是21,…,第六行的数是( )
如图,一根起点为0的数轴,现有同学将它弯折,弯折后虚线上第一行的数是0,第二行的数是6,第三行的数是21,…,第六行的数是( )| A. | 78 | B. | 120 | C. | 145 | D. | 171 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
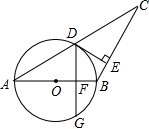 如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为A.作DG⊥AB交⊙O于G,垂足为F,若∠A=30°,AB=8.
如图,AB=BC,以AB为直径的⊙O交AC于点D,过D作DE⊥BC,垂足为A.作DG⊥AB交⊙O于G,垂足为F,若∠A=30°,AB=8.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点E,F是正方形ABCD的对角线BD所在直线上的两点,且BE=DF,∠EAB=15°.则$\frac{BE}{AB}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
如图,点E,F是正方形ABCD的对角线BD所在直线上的两点,且BE=DF,∠EAB=15°.则$\frac{BE}{AB}$=$\frac{\sqrt{6}-\sqrt{2}}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,⊙O的半径为3,过点A(5,0)的直线与⊙O相切于点B,与y轴正半轴相交于点C.
如图,⊙O的半径为3,过点A(5,0)的直线与⊙O相切于点B,与y轴正半轴相交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com