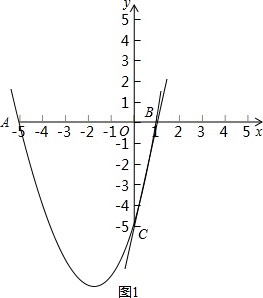
解:(1)由题意得:x
1+x
2=
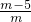
,x
1•x
2=

,x
2-x
1=6
则(x
1+x
2)
2-4x
1x
2=36,(
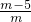
)
2+

=36
解得:m
1=1,m
2=-

.
经检验m=1,
∴抛物线的解析式为:y=x
2+4x-5
或:由mx
2-(m-5)x-5=0得,x=1或x=-

∵m>0,
∴1-

=6,
∴m=1.
∴抛物线的解析式为y=x
2+4x-5
由x
2+4x-5=0得x
1=-5,x
2=1
∴A(-5,0),B(1,0),C(0,-5).
设直线BC的解析式为y=kx+b,
则
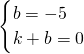
∴
∴直线BC的解析式为y=5x-5;
(2)如图1;
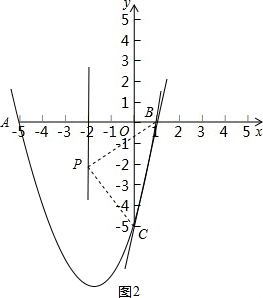
(3)如图2,由题意,圆心P在AB的中垂线上,即在抛物线y=x
2+4x-5的对称轴直线x=-2上,
设P(-2,-h)(h>0),
连接PB、PC,则PB
2=(1+2)
2+h
2,PC
2=(5-h)
2+2
2,
由PB
2=PC
2,
即(1+2)
2+h
2=(5-h)
2+2
2,解得h=2.
∴P(-2,-2),
∴⊙P的半径PB=
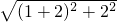
=

;
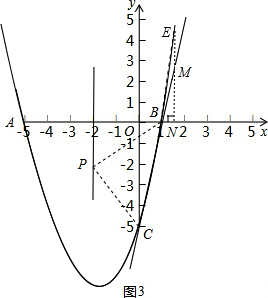
(4)如图3,设MN交直线BC于点E,点M的坐标为(t,t
2+4t-5),则点E的坐标为(t,5t-5).
若S
△MEB:S
△ENB=1:3,则ME:EN=1:3.
∴EN:MN=3:4,
∴t
2+4t-5=

(5t-5).
解得t
1=1(不合题意舍去),t
2=

,
∴M(
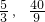
).
若S
△MEB:S
△ENB=3:1,则ME:EN=3:1.
∴EN:MN=1:4,
∴t
2+4t-5=4(5t-5).
解得t
3=1(不合题意舍去),t
4=15,
∴M(15,280).
∴存在点M,点M的坐标为(
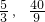
)或(15,280).
分析:(1)本题要先依据根与系数的关系表示出x
1+x
2、x
1•x
2的值,然后依据AB=6,即x
2-x
1=6来求出m的值,进而得出A、B两点的坐标.然后根据A、B、C的坐标用待定系数法求出抛物线和执行BC的解析式;
(2)经过选点、描点、连线画出函数图象即可;
(3)根据圆和抛物线的对称性可知:圆心P必在抛物线的对称轴上,因此可设出圆心P的纵坐标(其横坐标为抛物线对称轴的值),然后用坐标系中两点间的距离公式求出PB、PC的长,因为PB、PC均为半径,因此两者相等,由此可得出关于P点纵坐标的方程,即可求出P点的坐标;
(4)如果设MN与直线BC相交于E,本题要分两种情况进行讨论:
①S
△MEB:S
△ENB=1:3;②S
△MEB:S
△ENB=3:1.
可先根据直线BC的解析式设出E点的坐标,然后依据上面的分析的两种情况分别可得出一个关于E点坐标的方程,经过解方程即可得出E点的坐标.
点评:本题考查了一次函数和二次函数解析式的确定、一元二次方程根与系数的关系、三角形的外心、图形的面积的求法等知识点,主要考查了学生分类讨论、数形结合的数学思想方法.

 已知抛物线y=mx2-(m-5)x-5(m>0)与x轴交于两点A(x1,0)、B(x2,0)(x1<x2),与y轴交于点C,且AB=6.
已知抛物线y=mx2-(m-5)x-5(m>0)与x轴交于两点A(x1,0)、B(x2,0)(x1<x2),与y轴交于点C,且AB=6.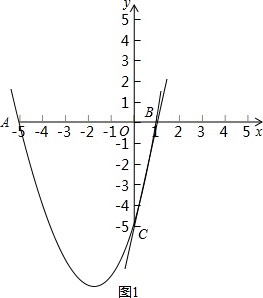 解:(1)由题意得:x1+x2=
解:(1)由题意得:x1+x2=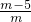 ,x1•x2=
,x1•x2= ,x2-x1=6
,x2-x1=6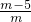 )2+
)2+ =36
=36 .
.
 =6,
=6,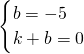
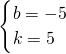
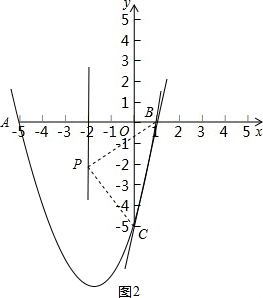
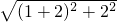 =
= ;
; (5t-5).
(5t-5). ,
,
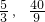 ).
).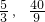 )或(15,280).
)或(15,280).

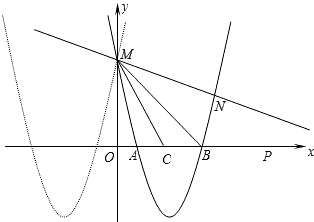 点N(a,b),a,b满足a2-a+m=0,b2-b+m=0,则点N的坐标为
点N(a,b),a,b满足a2-a+m=0,b2-b+m=0,则点N的坐标为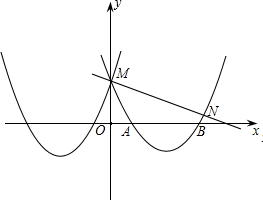 点M,与x轴交于点A和B.
点M,与x轴交于点A和B. 如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,并与y轴交于点M,与x轴交于点A和B.
如图,已知抛物线y=mx2+nx+p与y=x2+6x+5关于y轴对称,并与y轴交于点M,与x轴交于点A和B.