练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    7．某地区高效节能灯的年销售量2010年为10万只，预计2012年将达到14.4万只．则该地区2010年到2012年高效节能灯销售量的年平均增长率为（　　）
    A．10%B．20%C．30%D．40%

    分析 可以首先假设出增长率为x，这样2011年的销售量为10（1+x），2012年的销售量是在2011年的基础上再增长x，即10（1+x）×（1+x）=10（1+x）2，解出即可．

    解答 解：设该地区2010年到2012年高效节能灯年销售量的平均增长率为x，
    依据题意，列出方程10（1+x）2=14.4，
    整理得：（1+x）2=1.44，
    解得：x1=0.2，x2=-2.2（舍去），
    即可得该地区2010年到2012年高效节能灯年销售量的平均增长率为20%．
    故选B．

    点评 此题主要考查了如何求增长率问题，实际生活中这样的问题较多，也是中考中的一个热点问题，关键是根据题意列出一元二次方程．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    17．已知x-4的平方根是±2，y+21的立方根是3，求x2+y2的平方根．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

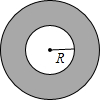    18． 如图，大圆的半径是R．
    （1）当小圆的面积是大圆面积的$\frac{4}{9}$时，求出阴影部分的面积；（用含R的代数式表示）
    （2）当小圆半径是大圆半径的一半时，且R=2cm，则阴影部分的面积为多少？（结果精确到0.1）参考数值：π≈3.14．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．计算：$\sqrt{12}÷\sqrt{\frac{1}{3}}$=6．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．一个不透明的袋子装有三个小球，它们除了分别标有数字1，3，5不同外，其他完全相同．
    （1）从袋中任意取出一个球，标号大于2的概率是多少？
    （2）若任意从袋子中摸出一球后放回，再任意摸出一球，则两次摸出的球所标数字之和为6的概率是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．先阅读，后解答：$\frac{{\sqrt{3}}}{{\sqrt{3}-\sqrt{2}}}=\frac{{\sqrt{3}（\sqrt{3}+\sqrt{2}）}}{{（\sqrt{3}-\sqrt{2}）（\sqrt{3}+\sqrt{2}）}}=\frac{{3+\sqrt{6}}}{{{{（\sqrt{3}）}^2}-{{（\sqrt{2}）}^2}}}=3+\sqrt{6}$，像上述解题过程中，$\sqrt{3}$-$\sqrt{2}$与
    $\sqrt{3}$+$\sqrt{2}$相乘积不含有二次根式，我们可将这两个式子称为互为有理化因式，上述解题过程也称为分母有理化．
    （1）$\sqrt{5}$+2的有理化因式是$\sqrt{5}$-2．
    （2）将$\frac{3}{{3+\sqrt{6}}}$进行分母有理化．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．有这样一道数学题：在等式y=ax2+bx+c中，当x=-1时，y=0，当x=2时，y=3，当x=5时，y=60．
    （1）请你列出关于a，b，c的方程组，这是一个三元一次方程组吗？
    （2）求出a，b，c的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    16．写出一个在第一象限的点A的坐标（1，2）；
    写出一个在第四象限的点B的坐标（2，-1）；
    写出一个在y轴上的点C的坐标（0，6）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

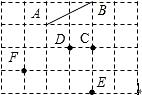    17．如图，在6×4的正方形网格中，点A、B、C、D、E、F都在格点上．连接点A、B得线段AB．
    （1）连接C、D、E、F中的任意两点，共可得6条线段，在图中画出来；
    （2）在（1）中所连得的线段中，与AB平行的线段是FD；
    （3）用三角尺或量角器度量、检验，AB及（1）中所连得的线段中，互相垂直的线段有几对？（请用“⊥”表示出来）CD⊥CE，DF⊥DE，AB⊥DE．

    查看答案和解析>>

    同步练习册答案