写出命题“等腰三角形两腰上的中线相等”的逆命题并对其进行证明.
逆命题:两边中线相等的三角形是等腰三角形.
已知:
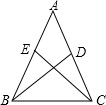
如图在△ABC中,BD、CE分别是边AC和AB上的中线,CE=BD,求证:△ABC是等腰三角形,
证明:
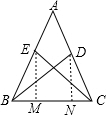
过E作EM⊥BC于M,过D作DN⊥BC于N,
∵BD、CE分别是边AC和AB上的中线,
∴S
△BEC=S
△BDC,
∴

BC×EM=

BC×DN,
∴EM=DN,
∵∠EMC=∠DNB=90°,
∴在Rt△EMC和Rt△DNB中,
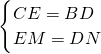
,
∴Rt△EMC≌Rt△DNB(HL),
∴∠ECB=∠DBC,
在△EBC和△DCB中,

,
∴△EBC≌△DCB(SAS),
∴∠EBC=∠DCB,
∴△ABC是等腰三角形.
分析:写出已知、求证、画出图形,过E作EM⊥BC于M,过D作DN⊥BC于N,求出EM=DN,证Rt△EMC≌Rt△DNB,推出∠ECB=∠DBC,证△EBC≌△DCB,推出∠EBC=∠DCB即可.
点评:本题考查了等腰三角形的判定,全等三角形的性质和判定的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的对应边相等,对应角相等.

 如图在△ABC中,BD、CE分别是边AC和AB上的中线,CE=BD,求证:△ABC是等腰三角形,
如图在△ABC中,BD、CE分别是边AC和AB上的中线,CE=BD,求证:△ABC是等腰三角形,
 BC×EM=
BC×EM= BC×DN,
BC×DN,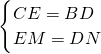 ,
, ,
,

 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案