
【题目】已知抛物线y=﹣![]() ﹣15有最高点(0,1),过点C(0,2)的直线l平行于x轴,O为坐标原点.
﹣15有最高点(0,1),过点C(0,2)的直线l平行于x轴,O为坐标原点.
(1)求m的值;
(2)求证:该抛物线上的任意一点到原点O的距离都等于这个点到直线l的距离;
(3)若点P,Q是抛物线上的任意两点,且PQ=9,点G是线段PQ的中点,求点G到直线l距离的最小值.
【答案】(1)m=4;(2)见解析;(3)4.5
【解析】
(1)由抛物线的顶点坐标为(0,1),可得m的值;
(2)设抛物线上的任意一点M(![]() ),则OM=
),则OM=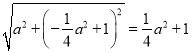 ,过点M作MN⊥l于N,可得MN=
,过点M作MN⊥l于N,可得MN=![]() =OM,则结论得证;
=OM,则结论得证;
(3)过点Q作QA⊥l于A,过点P作PB⊥l于B交l′于D,取DQ中点E,连接GE并延长交l于F,可得GF=![]() (AQ+BP),则GF=
(AQ+BP),则GF=![]() (OQ+OP),当点O,P,Q在同一直线上时,OQ+OP最小,求出点G到直线l距离的最小值为4.5.
(OQ+OP),当点O,P,Q在同一直线上时,OQ+OP最小,求出点G到直线l距离的最小值为4.5.
(1)∵抛物线的最高点为(0,1),
∴![]() ,
,
解得:m=4;
(2)由(1)得抛物线的解析式为![]() ,
,
设抛物线上的任意一点M(![]() ),
),
则OM=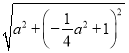
=![]()
=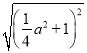
=![]() ,
,
过点M作MN⊥l于N,则MN=![]() =OM,
=OM,
∴抛物线上的任意一点到原点O的距离都等于这个点到直线l的距离;
(3)将直线l向下平移,使其经过点Q,设平移后的直线为l′,
如图,过点Q作QA⊥l于A,过点P作PB⊥l于B交l′于D,取DQ中点E,连接GE并延长交l于F,
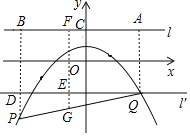
∵EG是△QDP的中位线,
∴GE∥DP,且EG=![]() ,
,
∴GE⊥l′,
易证:EF=AQ=BD,
∴GF=EF+EG=![]() (AQ+BD+DP),
(AQ+BD+DP),
=![]() (AQ+BP),
(AQ+BP),
由(2)得:AQ=OQ,BP=OP
∴GF=![]() (OQ+OP),
(OQ+OP),
∵当点O,P,Q在同一直线上时,OQ+OP最小,且最小值等于PQ=9,
∴![]() ,
,
∴点G到直线l距离的最小值为4.5.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
【题目】某农场去年种植了10亩地的南瓜,亩产量为2000![]() ,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
,根据市场需要,今年该农场扩大了种植面积,并且全部种植了高产的新品种南瓜,已知南瓜种植面积的增长率是亩产量的增长率的2倍,今年南瓜的总产量为60 000kg,求南瓜亩产量的增长率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1矩形ABCD中,点E是CD边上的动点(点E不与点C,D重合),连接AE,过点A作AF⊥AE交CB延长线于点F,连接EF,点G为EF的中点,连接BG.
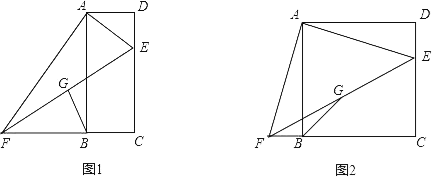
(1)求证:△ADE∽△ABF;
(2)若AB=20,AD=10,设DE=x,点G到直线BC的距离为y.
①求y与x的函数关系式;②当![]() 时,x的值为 ;
时,x的值为 ;
(3)如图2,若AB=BC,设四边形ABCD的面积为S,四边形BCEG的面积为S1,当![]() 时,DE:DC的值为 .
时,DE:DC的值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让同学们了解自己的体育水平,八年级![]() 班的体育老师对全班
班的体育老师对全班![]() 名学生进行了一次体育模拟测试(得分均为整数),成绩满分为
名学生进行了一次体育模拟测试(得分均为整数),成绩满分为![]() 分,
分,![]() 班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
班的体育委员根据这次测试成绩,制作了统计图和分析表如下:
八年级![]() 班全体女生体育测试成绩分布扇形统计图
班全体女生体育测试成绩分布扇形统计图
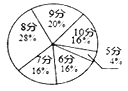
八年级全体男生体育测试成绩条形统计图
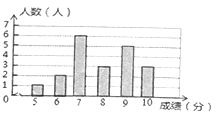
八年级![]() 班体育模拟测试成绩分析表
班体育模拟测试成绩分析表
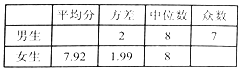
根据以上信息,解答下列问题:
(1)这个班共有男生 人,共有女生 人;
(2)补全八年级![]() 班体育模拟测试成绩分析表;
班体育模拟测试成绩分析表;
(3)你认为在这次体育测试中,![]() 班的男生队,女生队哪个表现更突出一些?并写出你的看法的理由.
班的男生队,女生队哪个表现更突出一些?并写出你的看法的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的顶点A,B,C的坐标分别是A(﹣1,﹣1),B(﹣4,﹣1),C(﹣4,﹣3).
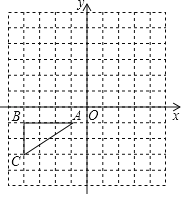
(1)作出△ABC关于原点O中心对称的图形△A1B1C1,并写出点B的对应点B1的坐标;
(2)作出△A1B1C1绕原点O顺时针旋转90°后的图形△A2B2C2,并写出点C1的对应点C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
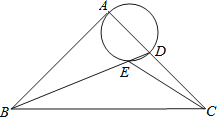
【题目】如图,在等腰Rt△ABC中,∠BAC=90°,AB=AC,BC=4![]() ,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为___.
,点D是AC边上一动点,连接BD,以AD为直径的圆交BD于点E,则线段CE长度的最小值为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】端午节放假期间,小明和小华准备到宜宾的蜀南竹海(记为A)、兴文石海(记为B)、夕佳山民居(记为C)、李庄古镇(记为D)的一个景点去游玩,他们各自在这四个景点中任选一个,每个景点都被选中的可能性相同.
(1)小明选择去蜀南竹海旅游的概率为 .
(2)用树状图或列表的方法求小明和小华都选择去兴文石海旅游的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在△ABC中,∠BAC>90°,点D为BC的中点,点E在AC上,将△CDE沿DE折叠,使得点C恰好落在BA的延长线上的点F处,连结AD,则下列结论不一定正确的是( )
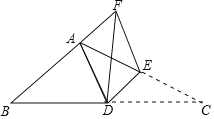
A. AE=EF B. AB=2DE
C. △ADF和△ADE的面积相等 D. △ADE和△FDE的面积相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D为边AC上的点,以AD为直径作⊙O,连接BD并延长交⊙O于点E,连接CE.
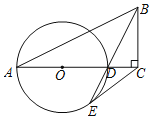
(1)若CE=BC,求证:CE是⊙O的切线.
(2)在(1)的条件下,若CD=2,BC=4,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com