Question

已知：抛物线y=-x²+（m+3）x-m-2与x轴交于A、B两点，与y轴交于C点．
（1）求m的取值范围；
（2）若m＞0，直线y=kx-1经过点A，与y轴交于点D，且AD•BD=2，求抛物线的解析式；
（3）在（2）的条件下：若A点在B点的左侧，P为所得的抛物线的顶点，PH⊥AB，H为垂足，连接PA，直线y=kx-1交x轴于M，若以O，D，M为顶点的三角形与与△HPA相似，请直接写出所有符合条件的M点的坐标．

Answer 1

解：（1）因为抛物线y=-x²+（m+3）x-m-2与x轴有两个交点，
所以方程x²-（m+3）x+（m+2）=0有两个不等实根，
所以△=[-（m+3）]²-4（m+2）=（m+1）²＞0，
所以m≠-1；

（2）设A（x₁，0）、B（x₂，0），
则x₁，x₂是方程x²+（m+1）x-（m+2）=0的两个实根，
∵x²-（m+3）x+（m+2）=（x-1）（x-m-2）=0，
∴x₁=1，x₂=m+2，
利用AD•BD=2，得：2[1+（m+2）²]=52，
解得m=-7和m=3，
∵m＞0，
∴m=3，
所求抛物线的解析式是y=-x²+6x-5；
（3）满足条件的点有四个：如图：

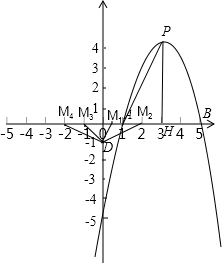
M₁（，0），M₂（2，0），M₃（-，0），M₄（-2，0）．
分析：（1）由于抛物线与x轴有两个不同的交点，可令y=0，则所得方程的根的判别式△＞0，可据此求出m的取值范围．
（2）根据已知直线的解析式，可得到D点的坐标；根据抛物线的解析式，可用m表示出A、B的坐标，即可得到AD、BD的长，代入AD×BD=2中，即可求得m的值，从而确定抛物线的解析式．
（3）根据（2）所给的条件求出A、B、D、P、H的坐标，再求出△HPA的三边长，最后根据以O，D，M为顶点的三角形与与△HPA相似求出OM的长，即可求出M点的坐标．
点评：此题考查了二次函数的综合；根据根的判别式、二次函数解析式的确定、勾股定理、函数图象的交点坐标及图形面积的求法进行解答，难度适中．