
分析 原式利用二次根式乘除法则,以及分母有理化法则计算即可得到结果.
解答 解:(1)原式=$\sqrt{8÷2}$=$\sqrt{4}$=2;
(2)原式=$\sqrt{6{a}^{3}b÷2ab}$=$\sqrt{3{a}^{2}}$=$\sqrt{3}$a;
(3)原式=$\frac{\sqrt{5}×\sqrt{3}}{\sqrt{3}×\sqrt{3}}$=$\frac{\sqrt{15}}{3}$;
(4)原式=$\frac{1}{\sqrt{3}}$×$\frac{1}{\sqrt{3}}$=$\frac{1}{3}$,
故答案为:(1)2;(2)$\sqrt{3}$a;(3)$\frac{\sqrt{15}}{3}$;(4)$\frac{1}{3}$
点评 此题考查了分母有理化,以及二次根式的乘除法,熟练掌握二次根式乘除法则及分母有理化法则是解本题的关键.


科目:初中数学 来源: 题型:选择题
 如图,在四边形ABCD中,AD∥BC,AC,BD交于点O,过点O作EF∥AD交AB于点E,F,若AE=2,BE=5,OD=3,则BD长为( )
如图,在四边形ABCD中,AD∥BC,AC,BD交于点O,过点O作EF∥AD交AB于点E,F,若AE=2,BE=5,OD=3,则BD长为( )| A. | 6 | B. | $\frac{15}{2}$ | C. | $\frac{21}{2}$ | D. | $\frac{10}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,⊙O的直径AB=10,CD是⊙O的弦,CD⊥AB,垂足为M,若OM:OB=3:5,则CD的长为( )
如图,⊙O的直径AB=10,CD是⊙O的弦,CD⊥AB,垂足为M,若OM:OB=3:5,则CD的长为( )| A. | 8 | B. | 6 | C. | 4 | D. | $\sqrt{91}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
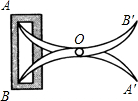 如图,将两根钢条AA′,BB′的中点O钉在一起,使AA′,BB′能绕点O自由转动,就做成一个测量工具,测A′B′的长即等于内槽宽AB,这种测量方法的依据是两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应边相等..
如图,将两根钢条AA′,BB′的中点O钉在一起,使AA′,BB′能绕点O自由转动,就做成一个测量工具,测A′B′的长即等于内槽宽AB,这种测量方法的依据是两边和它们的夹角分别相等的两个三角形全等,全等三角形的对应边相等..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点E、F、C、B在同一直线上,AB=DE,∠B=∠E,要判定△ABC≌△DEF,还需要添加一个条件,你添加的条件是EF=BC(或EC=BF或∠D=∠A或∠EFD=∠BCA 或∠DFB=∠ACE或DF∥AC).(写出一个即可)
如图,点E、F、C、B在同一直线上,AB=DE,∠B=∠E,要判定△ABC≌△DEF,还需要添加一个条件,你添加的条件是EF=BC(或EC=BF或∠D=∠A或∠EFD=∠BCA 或∠DFB=∠ACE或DF∥AC).(写出一个即可)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com