

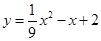 ;(2)①x=3,1;②P(3,0)或
;(2)①x=3,1;②P(3,0)或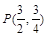 或
或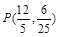 .
.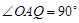 时,点P与点A重合,则P(3,0) ;当
时,点P与点A重合,则P(3,0) ;当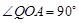 时,点P与点C重合,则x=0(不合题意);当
时,点P与点C重合,则x=0(不合题意);当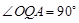 时,设PQ与
时,设PQ与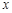 轴交于点D,先根据同角的余角相等证得△ODQ∽△QDA,根据相似三角形的性质可得
轴交于点D,先根据同角的余角相等证得△ODQ∽△QDA,根据相似三角形的性质可得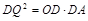 ,即可得到关于x的方程,从而求得结果.
,即可得到关于x的方程,从而求得结果.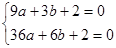 ,解得:
,解得: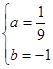
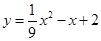 ;
;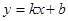 ,
,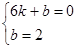 ,解得
,解得 ,
,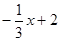
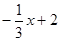 -(
-(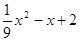 )=
)=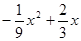 =
= .
.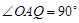 时,点P与点A重合,∴P(3,0)
时,点P与点A重合,∴P(3,0) 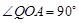 时,点P与点C重合,∴x=0(不合题意)
时,点P与点C重合,∴x=0(不合题意)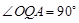 时,设PQ与
时,设PQ与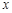 轴交于点D.
轴交于点D. 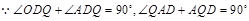 ,
,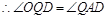 .
.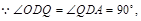
 ,即
,即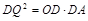 .
.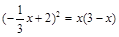 ,
,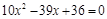 ,
,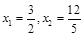 .
. 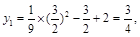
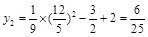 .
.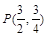 或
或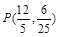 .
.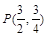 或
或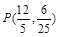 .
.

 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源:不详 题型:单选题
| x | -7 | -6 | -5 | -4 | -3 | -2 |
| y | -27 | -13 | -3 | 3 | 5 | 3 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
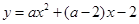 过点
过点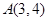 .
.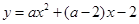 在直线
在直线 下方的部分沿直线
下方的部分沿直线 翻折,图象其余的部分保持不变,得到的新函数图象记为
翻折,图象其余的部分保持不变,得到的新函数图象记为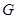 .点
.点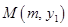 在图象
在图象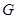 上,且
上,且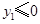 .
.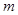 的取值范围;
的取值范围;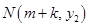 也在图象
也在图象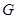 上,且满足
上,且满足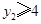 恒成立,则
恒成立,则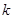 的取值范围为 .
的取值范围为 .查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
的图像与x轴、y轴的公共点分别为A(5,0)、B,点C在这个二次函数的图像上,且横坐标为3.
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
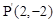 ,点A的对应点为
,点A的对应点为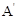 ,则抛物线上PA段扫过的区域(阴影部分)的面积为 .
,则抛物线上PA段扫过的区域(阴影部分)的面积为 .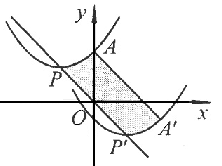
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
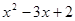 >0.解:令y=
>0.解:令y=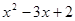 ,画出y=
,画出y=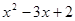 如图所示,
如图所示,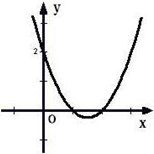
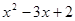 >0的解集为x<1或x>2.
>0的解集为x<1或x>2.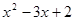 <0的解集为 ;
<0的解集为 ;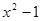 >0的解集为 ;
>0的解集为 ;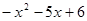 >0.
>0.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com