
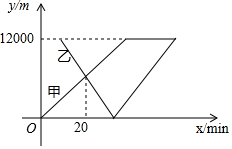
 甲旅游船上午9:00从嘉荫码头出发逆水而上匀速开往花骨山景区,10min后乙旅游船从龙骨山景区匀速返回嘉荫码头接送游客,游客上船后又立即起航开往龙骨山(游客上下船时间忽略不计),到达龙骨山时恰好10:00,此时甲船已到达20min,若甲船从码头出发后所用时间为x(单位:min),则甲、乙两船与嘉荫码头的距离y(单位:m)关于x的函数关系图象如图所示,请结合图象信息,解答下列问题:
甲旅游船上午9:00从嘉荫码头出发逆水而上匀速开往花骨山景区,10min后乙旅游船从龙骨山景区匀速返回嘉荫码头接送游客,游客上船后又立即起航开往龙骨山(游客上下船时间忽略不计),到达龙骨山时恰好10:00,此时甲船已到达20min,若甲船从码头出发后所用时间为x(单位:min),则甲、乙两船与嘉荫码头的距离y(单位:m)关于x的函数关系图象如图所示,请结合图象信息,解答下列问题:分析 (1)根据函数图象结合数量关系可分别求出乙船顺流与逆流的速度,二者做差除以2,即可得出水流的速度;
(2)找出乙船从龙骨山返回到码头时甲船航行的时间,再根据路程=速度×时间,即可得出结论;
(3)观察函数图象结合路程=速度×时间,即可得出在甲船行驶过程中,甲船与码头的距离y1关于时间x的函数解析式;
(4)根据函数图象可知:两船相遇时,乙船距嘉荫码头的距离等于甲船行驶的距离,再根据路程=速度×时间,即可得出结论;
(5)根据数量关系,找出乙船与码头的距离y2关于时间x的函数解析式为,分0≤x<10、10≤x<20、20≤x≤30、30<x≤40和40<x≤60五段,找出两船相距2000m的方程,解之即可得出结论.
解答 解:(1)甲船的逆水速度为12000÷(60-20)=300(米/分),
两船相遇时,甲船行驶了20分,乙船行驶了20-10=10(分),
乙船的顺水速度为(12000-20×300)÷10=600(米/分),
乙船从花骨山到嘉荫码头的时间为12000÷600=20(分),
乙船从嘉荫码头到花骨山的时间为60-10-20=30(分),
乙船的逆水速度为12000÷30=400(米/分),
∴水流速度为$\frac{1}{2}$(600-400)=100米/分;
(2)由(1)知乙船行20分,故甲船行20+10=30分,
∴300×(40-30)=3000(米),
∴乙船从龙骨山返回到码头时甲船距龙骨山3000米.
(3)当0≤x≤40时,y1=300x;
当x>40时,y1=12000.
∴甲船与码头的距离y1关于时间x的函数解析式为y1=$\left\{\begin{array}{l}{300x(0≤x≤40)}\\{12000(x>40)}\end{array}\right.$.
(4)两船相遇时,乙船距嘉荫码头的距离=甲船行驶的距离=300×20=6000(米).
(5)乙船与码头的距离y2关于时间x的函数解析式为y2=$\left\{\begin{array}{l}{12000(0≤x<10)}\\{12000-600(x-10)(10≤x≤30)}\\{400(x-30)(30<x≤60)}\end{array}\right.$,
当0≤x<10时,12000-300x=2000,
解得:x=$\frac{100}{3}$(舍去);
当10≤x<20时,12000-600(x-10)-300x=2000,
解得:x=$\frac{160}{9}$;
当20≤x≤30时,300x-[12000-600(x-10)]=2000,
解得:x=$\frac{200}{9}$;
当30<x≤40时,300x-400(x-30)=2000,
解得:x=100(舍去);
当40<x≤60时,12000-400(x-30)=2000,
解得:x=55.
综上所述:在乙船行驶过程中,甲船出发$\frac{160}{9}$、$\frac{200}{9}$、55分钟时两船相距2000m.
点评 本题考查了一次函数的应用以及解一元一次方程,解题的关键是:(1)根据数量关系,列式计算;(2)根据路程=速度×时间,列式计算;(3)路程=速度×时间,找出y1关于时间x的函数解析式;(4)观察函数图象,找出两船相遇时,乙船距嘉荫码头的距离等于甲船行驶的距离;(5)分0≤x<10、10≤x<20、20≤x≤30、30<x≤40和40<x≤60五段,找出关于x的一元一次方程.


科目:初中数学 来源: 题型:选择题
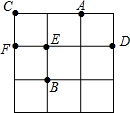 如图,在3×3的方格中,A,B,C,D,E,F分别位于格点上,从C,D,E,F四点中任意取一点,与点A,B为顶点作三角形,则所作三角形为等腰三角形的概率是( )
如图,在3×3的方格中,A,B,C,D,E,F分别位于格点上,从C,D,E,F四点中任意取一点,与点A,B为顶点作三角形,则所作三角形为等腰三角形的概率是( )| A. | 1 | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 (1)如图1,菱形ABCD中,O是对角线AC上一点,连接OB,OD,求证:OB=OD.
(1)如图1,菱形ABCD中,O是对角线AC上一点,连接OB,OD,求证:OB=OD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 套 | A种塑料(吨) | B种塑料(吨) | |
| M型滑梯 | 80-x | 0.6(80-x) | 0.9(80-x) |
| N型滑梯 | x | 1.1x | 0.4x |
| 合计 | 80 | 70 | 52 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,四边形ABCD为正方形,点A、B在y轴上,点C的坐标为(-4,1),反比例函数y=$\frac{k}{x}$的图象经过点D,则k的值为12.
如图,四边形ABCD为正方形,点A、B在y轴上,点C的坐标为(-4,1),反比例函数y=$\frac{k}{x}$的图象经过点D,则k的值为12.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com