
【题目】一个零件的形状如图所示,按规定∠A=90,∠C=25,∠B=25,检验员已量得∠BDC=150,请问:这个零件合格吗?说明理由。
【答案】解: 连接AD并延长,根据三角形的外角的性质得到∠CDE=∠C+∠CAD,∠BDE=∠B+∠DAB,计算出∠BDC的度数,比较即可.
这个零件不合格;
理由:如图,连接AD延长到E点,
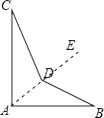
∵∠CDE是△ADC的外角,∠BDE是△ABD的外角,
∴∠CDE=∠C+∠CAD,∠BDE=∠B+∠DAB,
∴∠BDC=∠CDE+∠BDE=∠C+∠CAD+∠B+∠DAB,
即∠BDC=∠B+∠C+∠A=25°+25°+90°=140°,
但检验员已量得∠BDC=150°,
∴可以判断这个零件不合格
【解析】根据三角形的外角的性质得到∠CDE=∠C+∠CAD,∠BDE=∠B+∠DAB,计算出∠BDC的度数,比较即可.
【考点精析】关于本题考查的三角形的外角,需要了解三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(-1,0)、B(4,0)、C(0,2)三点.
(1)求该二次函数的解析式;
(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2,求S1-S2的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
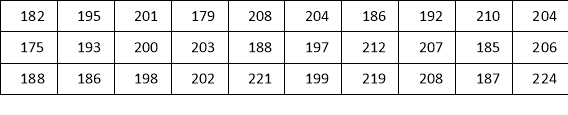
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:
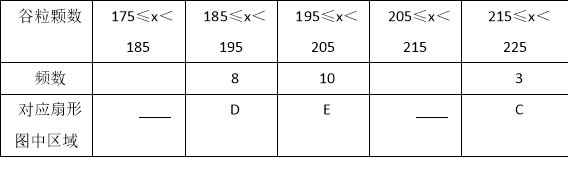
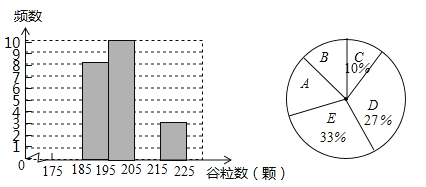
如图所示的扇形统计图中,扇形A对应的圆心角为 度,扇形B对应的圆心角为 度;
(2)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知二次函数![]() (a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为
(a、b、c为常数,a≠0)的图象过点O(0,0)和点A(4,0),函数图象最低点M的纵坐标为![]() ,直线l的解析式为y=x.
,直线l的解析式为y=x.
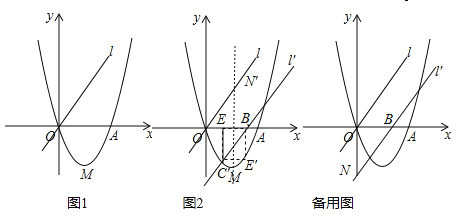
(1)求二次函数的解析式;
(2)直线l沿x轴向右平移,得直线l′,l′与线段OA相交于点B,与x轴下方的抛物线相交于点C,过点C作CE⊥x轴于点E,把△BCE沿直线l′折叠,当点E恰好落在抛物线上点E′时(图2),求直线l′的解析式;
(3)在(2)的条件下,l′与y轴交于点N,把△BON绕点O逆时针旋转135°得到△B′ON′,P为l′上的动点,当△PB′N′为等腰三角形时,求符合条件的点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,以AC为直径作⊙O交AB于点D,E为BC的中点,连接DE并延长交AC的延长线于点F.
(1)求证:DE是⊙O的切线;
(2)若CF=2,DF=4,求⊙O直径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+bx+c与x轴分别交于A(﹣1,0),B(5,0)两点.
(1)求抛物线的解析式;
(2)在第二象限内取一点C,作CD垂直X轴于点D,链接AC,且AD=5,CD=8,将Rt△ACD沿x轴向右平移m个单位,当点C落在抛物线上时,求m的值;
(3)在(2)的条件下,当点C第一次落在抛物线上记为点E,点P是抛物线对称轴上一点.试探究:在抛物线上是否存在点Q,使以点B、E、P、Q为顶点的四边形是平行四边形?若存在,请出点Q的坐标;若不存在,请说明理由.
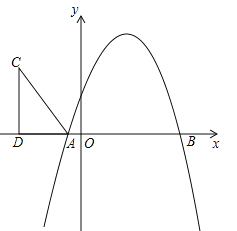
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com