练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，若数学公式的度数等于38°，求∠CBE+∠D的度数．

    解：连接BA，则∠ABE=×38°=19°，
    ∵四边形ABCD是圆内接四边形，
    ∴∠ABC+∠D=180°，
    ∴∠CBE+∠D=180°-19°=161°．
    分析：可以构造一个圆内接四边形，根据圆内接四边形的性质和圆周角定理进行求解．
    点评：此题要巧妙作辅助线，构造一个圆内接四边形．注意圆周角的度数等于它所对的弧的度数的一半．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

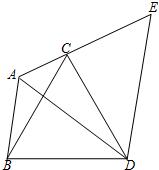    26、如图所示，△ABC的∠BAC=120°，以BC为边向形外作等边△BCD，把△ABD绕着D点按顺时针方向旋转60°到△ECD的位置，若AB=3，AC=2，求∠BAD的度数和线段AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    点D、E、F分别是△ABC的边AB、BC、CA的中点．如图所示，若以BD、BE为边分别作正△BMD和正△BEN，连接MF、FN、MN． 易证△FMN是等边三角形，因而∠MFN=60°；若以BD、BE为边分别作正方形BPMD和正方形BQNE，连接MF、NF、MN，则∠MFN的度数是
    90°
    90°
    ；若以BD、BE为边分别作正n边形，设两个正n边形与点D、E相邻的顶点分别是M、N（点M、N与点B是不同的点），连接MF、NF、MN得到△FMN，则∠MFN的度数是
    180°-
    360°
    n
    180°-
    360°
    n
    ．

    查看答案和解析>>

    科目：初中数学 来源：第26章《圆》常考题集（06）：26.1 旋转（解析版） 题型：解答题

    如图所示，△ABC的∠BAC=120°，以BC为边向形外作等边△BCD，把△ABD绕着D点按顺时针方向旋转60°到△ECD的位置，若AB=3，AC=2，求∠BAD的度数和线段AD的长．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年北京市五十五中九年级（上）第一次月考数学试卷（解析版） 题型：解答题

    如图所示，△ABC的∠BAC=120°，以BC为边向形外作等边△BCD，把△ABD绕着D点按顺时针方向旋转60°到△ECD的位置，若AB=3，AC=2，求∠BAD的度数和线段AD的长．

    查看答案和解析>>

    科目：初中数学 来源：《第23章 旋转》2010年五三中学自主学习达标检测（B）（解析版） 题型：解答题

    如图所示，△ABC的∠BAC=120°，以BC为边向形外作等边△BCD，把△ABD绕着D点按顺时针方向旋转60°到△ECD的位置，若AB=3，AC=2，求∠BAD的度数和线段AD的长．

    查看答案和解析>>

    同步练习册答案