
在平面直角坐标系中,已知函数 和函数
和函数 ,不论
,不论 取何值,
取何值, 都取
都取 与
与 二者之中的较小值.
二者之中的较小值.
1.求 关于
关于 的函数关系式
的函数关系式
2.现有二次函数 ,若函数
,若函数 和
和 都随着
都随着 的增大而减小,求自变
的增大而减小,求自变
量 的取值范围
的取值范围
3.在(2)的结论下,若函数 和
和 的图象有且只有一个公共点,求
的图象有且只有一个公共点,求 的取值范围.
的取值范围.
1.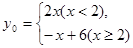 ……………………………………….……..2分
……………………………………….……..2分
(说明:两个自变量取值范围都含有等号或其中一个含等号均不扣分,都没等号扣1分)
2. 对函数
对函数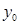 ,当
,当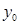 随
随 的增大而减小,
的增大而减小,
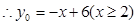 ,
………………………………………..…….3分
,
………………………………………..…….3分
又 函数
函数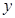 的对称轴为直线
的对称轴为直线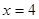 ,
…………………………….……..4分
,
…………………………….……..4分
且 ,
,
 当
当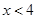 时,
时,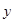 随
随 的增大而减小,
………………………….……..5分
的增大而减小,
………………………….……..5分

 …………………………………….…………….…..6分
…………………………………….…………….…..6分
3.①若函数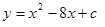 与
与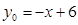 只有一个交点,且交点在
只有一个交点,且交点在 范围内.
范围内.
则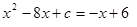 ,
,
 ,
,
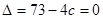 ,
,
得 …………………………….…………….…7分
…………………………….…………….…7分
此时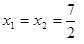 ,符合
,符合 , ………….…………..….…8分
, ………….…………..….…8分

②若函数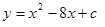 与
与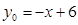 有两个交点,其中一个在
有两个交点,其中一个在 范围内,另一个交点在
范围内,另一个交点在 范围外.则
范围外.则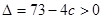 , 即
, 即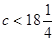 , ………….…9分
, ………….…9分
方法一: 对
对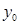 ,当
,当 时
时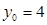 ;当
;当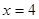 时
时 .
.
又 当
当 时,
时,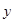 随
随 的增大而减小,
……….………10分
的增大而减小,
……….………10分
若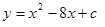 与
与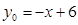 在
在 内有一个交点,
内有一个交点,
则当 时
时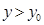 ;当
;当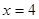 时
时 ,
,
即当 时
时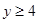 ;当
;当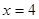 时
时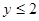 .
.
也即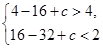 解得
解得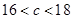 ,
……….……..…11分
,
……….……..…11分
由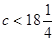 ,得
,得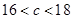 …………………………..…12分
…………………………..…12分
综上所述,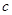 的取值范围是:
的取值范围是: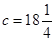 或
或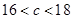 .
.
方法二:由函数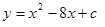 与
与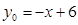 的一个交点在
的一个交点在 范围内,另一个交点在
范围内,另一个交点在 范围外,可得:
范围外,可得: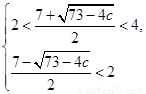 或
或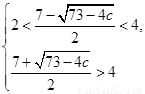
解第一个不等式组,可得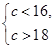 即无解;
…….………10分
即无解;
…….………10分
解第二个不等式组,可得 即
即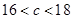 ,
….………11分
,
….………11分
由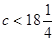 ,得
,得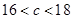 .
……………………………..…12分
.
……………………………..…12分
【解析】(1)有题意可知y1和y2交于(2,4),当x小于2时,y1和y2中y1较小,当x大于2时,y1和y2中y2较小,当x=2时,y1=y2,因此,y0是关于x的分段函数,当x<2时,y0=-x+6,当x>2时,y0=2x
(2)因为对函数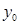 ,当
,当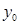 随
随 的增大而减小,所以y0=-x+6, 函数
的增大而减小,所以y0=-x+6, 函数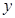 的对称轴为直线
的对称轴为直线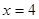 ,且
,且 ,所以自变量
,所以自变量 的取值范围
的取值范围
(3)分两种情况讨论:①若函数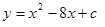 与
与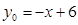 只有一个交点,且交点在
只有一个交点,且交点在 范围内.;②若函数
范围内.;②若函数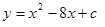 与
与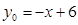 有两个交点,其中一个在
有两个交点,其中一个在 范围内,另一个交点在
范围内,另一个交点在 范围外
范围外


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
坐标原点.A、B两点的横坐标分别是方程x2-4x-12=0的两根,且cos∠DAB=
| ||
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.
18、在平面直角坐标系中,把一个图形先绕着原点顺时针旋转的角度为θ,再以原点为位似中心,相似比为k得到一个新的图形,我们把这个过程记为【θ,k】变换.例如,把图中的△ABC先绕着原点O顺时针旋转的角度为90°,再以原点为位似中心,相似比为2得到一个新的图形△A1B1C1,可以把这个过程记为【90°,2】变换.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com