

 ,
, (x-3)2;
(x-3)2;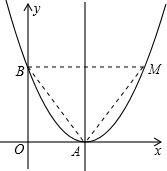 ∵四边形OAMB的四边长是四个连续的正整数,其中有3、4,
∵四边形OAMB的四边长是四个连续的正整数,其中有3、4, (4-3)2=
(4-3)2= (不是整数,舍去);
(不是整数,舍去); (不是整数,舍去);
(不是整数,舍去); (m-3)2,
(m-3)2,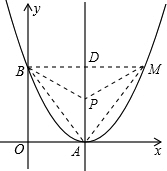 则PA=|t|,PD=|4-t|,PM2=PB2=(4-t)2+9,
则PA=|t|,PD=|4-t|,PM2=PB2=(4-t)2+9, )2+
)2+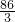 ,
, 时,PA2+PB2+PM2有最小值
时,PA2+PB2+PM2有最小值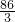 ;
; (m-3)2,由于m、n同为正整数,因此m-3应该是3的倍数,即m应该取3的倍数,可据此求出m、n的值,再根据“以M、B、O、A为顶点的四边形四条边的长度是四个连续的正整数”将不合题意的解舍去,即可得到M点的坐标;
(m-3)2,由于m、n同为正整数,因此m-3应该是3的倍数,即m应该取3的倍数,可据此求出m、n的值,再根据“以M、B、O、A为顶点的四边形四条边的长度是四个连续的正整数”将不合题意的解舍去,即可得到M点的坐标;

科目:初中数学 来源: 题型:
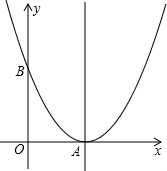
查看答案和解析>>
科目:初中数学 来源:第34章《二次函数》中考题集(30):34.4 二次函数的应用(解析版) 题型:解答题
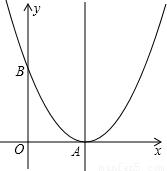
查看答案和解析>>
科目:初中数学 来源:第2章《二次函数》中考题集(28):2.3 二次函数的应用(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2008-2009学年山东省临沂市费县九年级(上)期末数学试卷(解析版) 题型:解答题
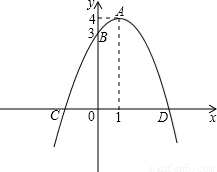
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com