
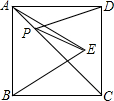
 如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为6.
如图所示,正方形ABCD的边长为6,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为6. 科目:初中数学 来源: 题型:解答题
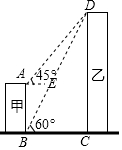 如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,求这两座建筑物的高度(结果保留根号)
如图,甲、乙为两座建筑物,它们之间的水平距离BC为30m,在A点测得D点的仰角∠EAD为45°,在B点测得D点的仰角∠CBD为60°,求这两座建筑物的高度(结果保留根号)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y3<y2,y1<y2 | B. | y1<y2<y3 | C. | y1>y2>y3 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
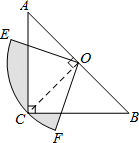 如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4$\sqrt{2}$,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,$\widehat{EF}$经过点C,则图中阴影部分的面积为( )
如图,在△ABC中,∠C=90°,AC=BC,斜边AB=4$\sqrt{2}$,O是AB的中点,以O为圆心,线段OC的长为半径画圆心角为90°的扇形OEF,$\widehat{EF}$经过点C,则图中阴影部分的面积为( )| A. | 2π-4 | B. | 4-π | C. | π-2 | D. | 4π-8 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com