Question

两个同心圆的半径分别是5cm和4cm，大圆的一条长为8cm的弦AB与小圆相交于C、D两点，则CD=    cm．

Answer 1

【答案】分析：作出两同心圆，过圆心作弦AB的垂线，构成直角三角形，然后用勾股定理计算求出CD的长．
解答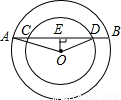：解：如图：OA=5，OD=4，AB=8，过O作OE⊥AB于E，则AE=EB=4，CE=CD，
在Rt△OAE中，OE²=0A²-AE²=25-16=9．
在Rt△ODE中，DE²=OD²-0E²=16-9=7．
∴DE=
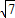
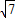
∴CD=2cm．
故答案是：2．
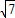
点评：本题考查的是垂径定理，根据垂径定理，过圆心O作弦的垂线，连接OA，OD，得到两个直角三角形，在直角三角形中，用勾股定理计算可以求出弦CD的长．