
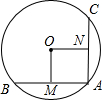
 如图,⊙O的弦AB⊥AC,AB=AC,OM⊥AB,ON⊥AC,垂足分别为M、N,若AB=2,则⊙O的半径为________.
如图,⊙O的弦AB⊥AC,AB=AC,OM⊥AB,ON⊥AC,垂足分别为M、N,若AB=2,则⊙O的半径为________.
 AB,AN=CN=
AB,AN=CN= AC,根据垂直定义得到∠A=∠OMA=∠ONA=90°,得出正方形OMAN,求出ON=CN=1,根据勾股定理即可求出答案.
AC,根据垂直定义得到∠A=∠OMA=∠ONA=90°,得出正方形OMAN,求出ON=CN=1,根据勾股定理即可求出答案.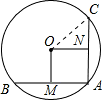 解:如图,连接OC,
解:如图,连接OC, AB=1,AN=CN=
AB=1,AN=CN= AC=1,
AC=1, =
= .
. .
.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com