
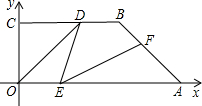
如图,直角梯形OABC中,AB∥OC,O为坐标原点,点A在y轴正半轴上,点C在x轴正半轴上,点B坐标为(2, ),∠BCO=60°,OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒.
),∠BCO=60°,OH⊥BC于点H.动点P从点H出发,沿线段HO向点O运动,动点Q从点O出发,沿线段OA向点A运动,两点同时出发,速度都为每秒1个单位长度.设点P运动的时间为t秒.
(1)求OH的长;
(2)若△OPQ的面积为S(平方单位).求S与t之间的函数关系式.并求t为何值时,△OPQ的面积最大,最大值是多少;
(3)设PQ与OB交于点M.①当△OPM为等腰三角形时,求(2)中S的值. ②探究线段OM长度的最大值是多少,直接写出结论.
2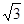 ;
;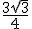 ;
;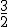
解析试题分析:(1)∵AB∥OC
∴∠OAB=∠AOC=90°
在Rt△OAB中,AB=2,AO=2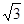
∴OB=4,∠ABO=60°
∴∠BOC=60°而∠BCO=60°
∴△BOC为等边三角形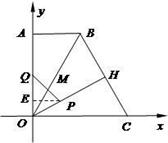
∴OH=OBcos30°=4× =2
=2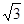 ; 2分
; 2分
(2)∵OP="OH-PH=2" 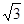 -t
-t
∴Xp="OPcos30°=3-"  t Yp="OPsin30°="
t Yp="OPsin30°=" 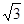 -
- 
∴S=  •OQ•Xp=
•OQ•Xp= 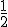 •t•(3-
•t•(3- t)
t)
=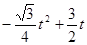 (o<t<2
(o<t<2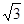 )
)
当t=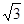 时,S最大=
时,S最大= 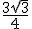 ; 5分
; 5分
(3)①若△OPM为等腰三角形,则:
(i)若OM=PM,∠MPO=∠MOP=∠POC
∴PQ∥OC
∴OQ=yp即t= 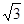 -
- 
解得:t=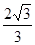
此时S=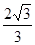
(ii)若OP=OM,∠OPM=∠OMP=75°∴∠OQP=45°
过P点作PE⊥OA,垂足为E,则有:EQ=EP
即t-(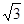 -
- 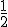 t)="3-"
t)="3-"  t
t
解得:t=2
此时S=
(iii)若OP=PM,∠POM=∠PMO=∠AOB∴PQ∥OA
此时Q在AB上,不满足题意. 10分
②线段PM长的最大值为 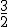 . 12分
. 12分
考点:二次函数的综合题
点评:此题将用待定系数法求二次函数解析式、动点问题和最小值问题相结合,有较大的思维


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
| 1 |
| 4 |
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=
如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=| k |
| x |
| BF |
| OA |
| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
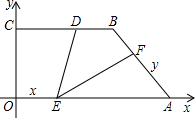 是BC上一点,BD=
是BC上一点,BD=| 1 |
| 4 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 2 |
| 3 |
| 2 |
| 2 |
| 3 |
| 2 |
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com