
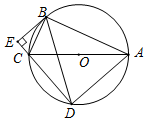
 如图,⊙O是△ABC的外接圆,AC为直径,弦ED=BA,BE⊥DC交DC的延长线于点E,求证:
如图,⊙O是△ABC的外接圆,AC为直径,弦ED=BA,BE⊥DC交DC的延长线于点E,求证:分析 (Ⅰ)由四边形ABCD为圆的内角四边形,得到四边形外角等于它的内对角,得证;
(Ⅱ)连接OB,OD,利用SSS得到三角形ABO与三角形DBO全等,利用全等三角形对应角相等得到∠DBO=∠ABO,进而确定出一对内错角相等,得到OB与ED平行,由BE与ED垂直,得到EB与BO垂直,即可得证.
解答 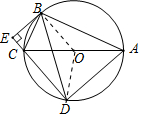 (Ⅰ)证明:∵四边形ABCD是圆内接四边形,
(Ⅰ)证明:∵四边形ABCD是圆内接四边形,
∴∠ECB=∠BAD;
(Ⅱ)证明:连结OB,OD,
在△ABO和△DBO中,
$\left\{\begin{array}{l}{AB=BD}\\{BO=BO}\\{OA=OD}\end{array}\right.$,
∴△ABO≌△DBO(SSS),
∴∠DBO=∠ABO,
∵∠ABO=∠OAB=∠BDC,
∴∠DBO=∠BDC,
∴OB∥ED,
∵BE⊥ED,
∴EB⊥BO,
∴BE是⊙O的切线.
点评 此题考查了切线的判定,以及圆内接四边形的性质,熟练掌握切线的判定方法是解本题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -($\frac{3}{4}$x+1)=5 | B. | -$\frac{3}{4}$x+1=5 | C. | $\frac{3}{4}$x-1=5 | D. | -x($\frac{3}{4}$x+1)=5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同,他们将一头骆驼前两昼夜的体温变化情况绘制成右图,请根据图象回答:
某生物兴趣小组在四天的实验研究中发现:骆驼的体温会随外部环境温度的变化而变化,而且在这四天中每昼夜的体温变化情况相同,他们将一头骆驼前两昼夜的体温变化情况绘制成右图,请根据图象回答:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
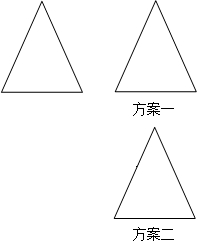 张倩同学打算制作一个平行四边形纸板,但手中只有一块等腰三角形纸板.张倩同学想了一下,用剪刀只剪了一刀,便得到一个平行四边形,且纸板充分利用没有浪费.你知道张倩是怎样剪的吗?用虚线表示出剪刀线;并请你画出两种张倩所拼的平行四边形.
张倩同学打算制作一个平行四边形纸板,但手中只有一块等腰三角形纸板.张倩同学想了一下,用剪刀只剪了一刀,便得到一个平行四边形,且纸板充分利用没有浪费.你知道张倩是怎样剪的吗?用虚线表示出剪刀线;并请你画出两种张倩所拼的平行四边形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com