解:(1)直线
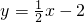
中,令y=0,则x=4;令x=0,则y=-2;
故B(4,0),C(0,-2);
由于抛物线经过点C(0,-2),故c=-2;
将B点坐标代入y=

x
2-bx-2中,得:b=-

;
∴抛物线的解析式为
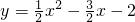
.
(2)根据(1)中的函数解析式可知A(-1,0),B(4,0),C(0,-2);
则AB=5,AC=

,BC=2

;
故AC
2+BC
2=5+20=25=AB
2,
∴△ABC是直角三角形,且∠ACB=90°.
(3)分两种情况考虑:
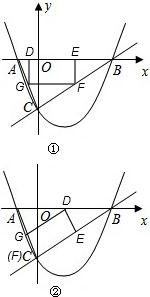
①如图①所示,矩形DEFG中D、E在AB边上;
设DG=EF=m;
由于FG∥x轴,则△CGF∽△CAB,

,
解得FG=5-

m;
故矩形的面积S=DG•FG=(5-

m)m=-

m
2+5m,
即S=-

(m-1)
2+

,
故m=1时,矩形的面积最大为2.5;
此时D(-

,0),E(2,0),G(-

,-1),F(2,-1);
②如图②所示,矩形DEFG中,F、C重合,D在AB边上;
设DE=CG=n,同①可得:
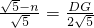
即DG=2

-2n;
故矩形的面积S=DE•DG=(2

-2n)n=-2(n-

)
2+

;
即当n=

时,矩形的最大面积为2.5;
此时BD=5×
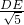
=

,OD=OB-BD=

,
即D(

,0);
综上所述,矩形的最大面积为2.5,此时矩形在AB边上的顶点坐标为(-

,0),(2,0)或(

,0).
分析:(1)根据直线BC的解析式,可确定B、C的坐标,代入抛物线的解析式中,即可确定待定系数的值.
(2)由(1)得到的抛物线解析式,可求得A点的坐标,进而可得到AB、AC、BC的长,然后根据这三边的长,来判断△ABC的形状.
(3)此题应分两种情况考虑:
①矩形有两个顶点在AB边上(设这两点为D、E),首先设出DG的长为m,利用相似三角形△CFG∽△CBA得到的比例线段,可求得GF的表达式,进而可根据矩形的面积公式求出关于矩形的面积和m的函数关系式,根据函数的性质即可得到矩形的最大面积及对应的m值,从而确定出矩形的四顶点的坐标;
②矩形有一个顶点在AB边上(设为D),此时C、F重合,方法同①,首先设DE=n,由△ADG∽△ABC求出DG的长,进而根据矩形的面积公式得到关于矩形的面积和n的函数关系式,从而根据函数的性质求得矩形的最大面积和对应的n值,进而确定矩形的四个顶点坐标.
点评:此题考查了二次函数解析式的确定、直角三角形的判定、矩形面积的计算方法、二次函数最值的应用等知识,要注意(3)题中,矩形的摆放方法有两种,不要漏解.

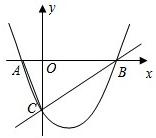
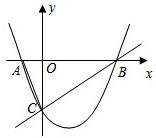 如图1,已知:抛物线
如图1,已知:抛物线 与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是
与x轴交于A、B两点,与y轴交于点C,经过B、C两点的直线是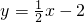 ,连接AC.
,连接AC. }.
}.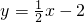 中,令y=0,则x=4;令x=0,则y=-2;
中,令y=0,则x=4;令x=0,则y=-2; x2-bx-2中,得:b=-
x2-bx-2中,得:b=- ;
;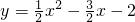 .
. ,BC=2
,BC=2 ;
;
 ,
, m;
m; m)m=-
m)m=- m2+5m,
m2+5m, (m-1)2+
(m-1)2+ ,
, ,0),E(2,0),G(-
,0),E(2,0),G(- ,-1),F(2,-1);
,-1),F(2,-1);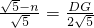
 -2n;
-2n; -2n)n=-2(n-
-2n)n=-2(n- )2+
)2+ ;
; 时,矩形的最大面积为2.5;
时,矩形的最大面积为2.5;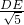 =
= ,OD=OB-BD=
,OD=OB-BD= ,
, ,0);
,0); ,0),(2,0)或(
,0),(2,0)或( ,0).
,0).

 如图1,已知:抛物线y=
如图1,已知:抛物线y=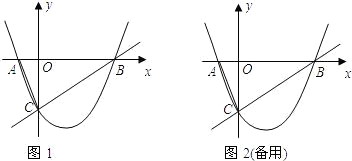

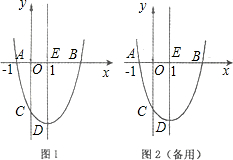
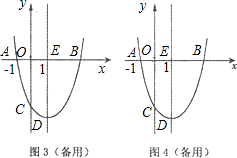
 与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是
与x轴交于A,B两点,与y轴交于点C,经过B,C两点的直线是 ,连结AC.
,连结AC.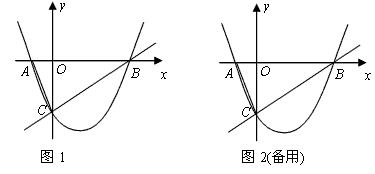
 的顶点坐标是
的顶点坐标是 ]
]