
如图,△PQR是⊙O的内接正三角形,四边形ABCD是⊙O的内接正方形,BC∥QR,则∠AOQ的度数为( )
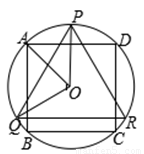
A.60° B. 65° C. 72° D. 75°
D.
【解析】
试题分析:作辅助线连接OD,根据题意求出∠POQ和∠AOD的,利用平行关系求出∠AOP度数,即可求出∠AOQ的度数.
连接OD,AR,
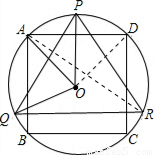
∵△PQR是⊙O的内接正三角形,
∴∠PRQ=60°,
∴∠POQ=2×∠PRQ=120°,
∵四边形ABCD是⊙O的内接正方形,
∴△AOD为等腰直角三角形,
∴∠AOD=90°,
∵BC∥RQ,AD∥BC,
∴AD∥QR,
∴∠ARQ=∠DAR,
∴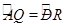 ,
,
∵△PQR是等边三角形,
∴PQ=PR,
∴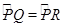 ,
,
∴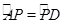 ,
,
∴∠AOP=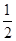 ∠AOD=45°,
∠AOD=45°,
所以∠AOQ=∠POQ-∠AOP=120°-45°=75°.
故选D.
考点: 正多边形和圆.


 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案科目:初中数学 来源: 题型:
 如图:△PQR是等边三角形,∠APB=120°
如图:△PQR是等边三角形,∠APB=120°| 7 |
| 14 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,△PQR是△ABC经过某种变换得到的图形,点A与点P、点B与点Q、点C与点R是对应点,观察它们之间的关系,设第一象限内的点M的坐标为(m,n);
如图,△PQR是△ABC经过某种变换得到的图形,点A与点P、点B与点Q、点C与点R是对应点,观察它们之间的关系,设第一象限内的点M的坐标为(m,n);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com