
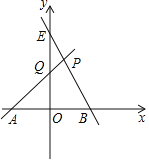
【题目】如图,已知直线AQ与x轴负半轴交于点A,与y轴正半轴交于点Q,∠QAO=45°,直线AQ在y轴上的截距为2,直线BE:y=-2x+8与直线AQ交于点P.
(1)求直线AQ的解析式;
(2)在y轴正半轴上取一点F,当四边形BPFO是梯形时,求点F的坐标.
(3)若点C在y轴负半轴上,点M在直线PA上,点N在直线PB上,是否存在以Q、C、M、N为顶点的四边形是菱形,若存在请求出点C的坐标;若不存在请说明理由.
【答案】(1)直线AQ的解析式为y=x+2;(2)F(0,4);(3)存在,C(0,![]() )或C(0,-10)
)或C(0,-10)
【解析】
(1)利用待定系数法即可求出直线AQ的解析式;
(2)先求出直线AQ和直线BE的交点P的坐标,由PF∥x轴可知F横坐标为0,纵坐标与点P的纵坐标相等;
(3)分CQ为菱形的对角线与CQ是菱形的一条边两种情况讨论.
解:(1)设直线AQ的解析式为y=kx+b,
∵直线AQ在y轴上的截距为2,
∴b=2,
∴直线AQ的解析式为y=kx+2,
∴OQ=2,
在Rt△AOQ中,∠OAQ=45°,
∴OA=OQ=2,
∴A(-2,0),
∴-2k+2=0,
∴k=1,
∴直线AQ的解析式为y=x+2;
(2)由(1)知,直线AQ的解析式为y=x+2①,
∵直线BE:y=-2x+8②,
联立①②解得![]() ,
,
∴P(2,4),
∵四边形BPFO是梯形,
∴PF∥x轴,
∴F(0,4);
(3)设C(0,c),
∵以Q、C、M、N为顶点的四边形是菱形,
①当CQ是对角线时,CQ与MN互相垂直平分,
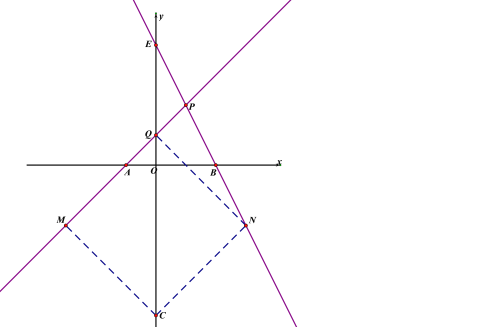
设C(0,c),
∵CQ的中点坐标为(0,![]() ),
),
∴点M,N的纵坐标都是![]() ,
,
∴M(![]() ,
,![]() ),N(
),N(![]() ,
,![]() ),
),
∴![]() +
+![]() =0,
=0,
∴c=-10,
∴C(0,-10),
②当CQ为边时,CQ∥MN,CQ=MN=QM,
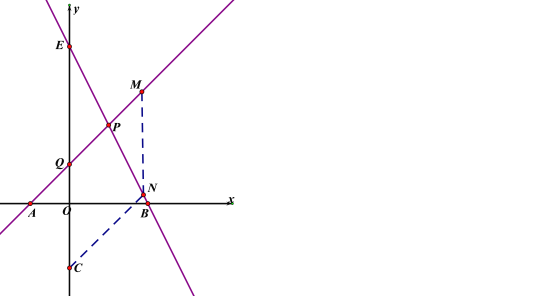
设M(m,m+2),
∴N(m,-2m+8),
∴|3m-6|=2-c=![]() |m|,
|m|,
∴m=![]() 或m=
或m=![]() ,
,
∴c=![]() 或c=
或c=![]() (舍),
(舍),
∴![]() ,
,
∴(0,![]() )或C(0,-10).
)或C(0,-10).


科目:初中数学 来源: 题型:
【题目】某汽车销售公司经销某品牌A款汽车,随着汽车的普及,其价格也在不断下降.今年5月份A款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的A款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份A款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的B款汽车,已知A款汽车每辆进价为7.5万元,B款汽车每辆进价为6万元,公司预计用不多于105万元且不少于99万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)如果B款汽车每辆售价为8万元,为打开B款汽车的销路,公司决定每售出一辆B款汽车,返还顾客现金a万元,要使(2)中所有的方案获利相同,a值应是多少?此时,哪种方案对公司更有利?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】填空,完成下列说理过程
如图,点A,O,B在同一条直线上,OD,OE分别平分∠AOC和∠BOC.
(1)求∠DOE的度数;
(2)如果∠COD=65°,求∠AOE的度数.

解:(1)如图,因为OD是∠AOC的平分线,
所以∠COD=![]() ∠AOC.
∠AOC.
因为OE是∠BOC的平分线,
所以∠COE=![]() .
.
所以∠DOE=∠COD+ =![]() (∠AOC+∠BOC)=
(∠AOC+∠BOC)=![]() ∠AOB= °.
∠AOB= °.
(2)由(1)可知
∠BOE=∠COE= ﹣∠COD= °.
所以∠AOE= ﹣∠BOE= °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下面材料:
在数轴上2与﹣1所对的两点之间的距离:|2﹣(﹣1)|=3;
在数轴上﹣2与3所对的两点之间的距离:|﹣2﹣3|=5;
在数轴上﹣3与﹣1所对的两点之间的距离:|(﹣1)﹣(﹣3)|=2
归纳:在数轴上点A、B分别表示数a、b,则A、B两点之间的距离AB=|a﹣b|或|b﹣a|

回答下列问题:
(1) 数轴上表示数x和1的两点之间的距离表示为 ;数轴上表示数x和 的两点之间的距离表示为|x+2|;
(2)请你在草稿纸上画出数轴,当表示数x的点在﹣2与3之间移动时,|x﹣3|+|x+2|的值总是一个固定的值为: .
(3)继续请你在草稿纸上画出数轴,探究当x=_______时,|x-3|+|x+2|=7.
查看答案和解析>>
科目:初中数学 来源: 题型:
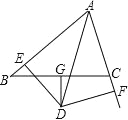
【题目】如图,G 为 BC 的中点,且 DG⊥BC,DE⊥AB 于 E,DF⊥AC 于 F, BE=CF.
(1)求证:AD 是∠BAC 的平分线;
(2)如果 AB=8,AC=6,求 AE 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
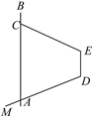
【题目】如图所示,已知射线 DM与直线AB交于点A,线段EC与直线AB交于点C,AB∥DE.
(1)当∠MAC=100°,∠BCE=120°时,把EC绕点E旋转多大角度(所求角度小于180°)时,可判定MD∥EC?请你设计出两种方案,并画出草图;
(2)若将EC绕点E逆时针旋转60°时,点C与点A恰好重合,请画出草图,并在图中找出同位角、内错角各两对(先用数字标出角,再回答).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com