
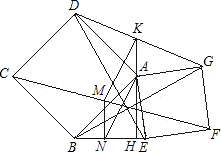
 如图,两个正方形ABCD和AEFG共顶点A,连BE,DG,CF,AE,BG,K,M分别为DG和CF的中点,KA的延长线交BE于H,MN⊥BE于N.则下列结论:①BG=DE且BG⊥DE;②△ADG和△ABE的面积相等;③BN=EN,④四边形AKMN为平行四边形.其中正确的是
如图,两个正方形ABCD和AEFG共顶点A,连BE,DG,CF,AE,BG,K,M分别为DG和CF的中点,KA的延长线交BE于H,MN⊥BE于N.则下列结论:①BG=DE且BG⊥DE;②△ADG和△ABE的面积相等;③BN=EN,④四边形AKMN为平行四边形.其中正确的是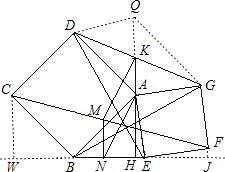 解:由两个正方形的性质易证△AED≌△AGB,
解:由两个正方形的性质易证△AED≌△AGB, (CW+FJ)=
(CW+FJ)= WC=
WC= (BH+HE)=
(BH+HE)= BE;
BE; AQ=
AQ= BE,
BE, S?ADQG,②正确.
S?ADQG,②正确.

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com