
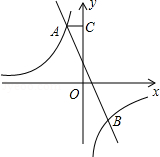
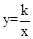 和直线y=mx+n交于点A和B,B点的坐标是(2,﹣3),AC垂直y轴于点C,AC=
和直线y=mx+n交于点A和B,B点的坐标是(2,﹣3),AC垂直y轴于点C,AC=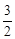 .
.
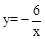 , y=﹣2x+1(2)
, y=﹣2x+1(2)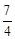
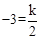 ,解得k=﹣6。
,解得k=﹣6。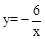 。
。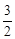 ,∴点A的横坐标是﹣
,∴点A的横坐标是﹣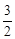 ,∴点A的横坐标
,∴点A的横坐标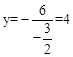 。
。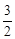 ,4)。
,4)。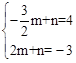 ,解得
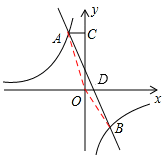
,解得 。
。
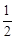 ,∴点D的坐标为(
,∴点D的坐标为(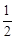 ,0)。∴OD=
,0)。∴OD=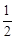 。
。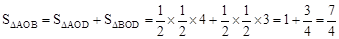 。
。 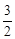 可得点A的横坐标,然后求出点A的坐标,再利用待定系数法求函数解析式求解直线的解析式。
可得点A的横坐标,然后求出点A的坐标,再利用待定系数法求函数解析式求解直线的解析式。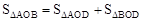 ,列式计算即可得解
,列式计算即可得解

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源:不详 题型:解答题
 O
O 中,梯形AOBC的边OB在
中,梯形AOBC的边OB在 轴的正半轴上,AC//OB,BC⊥OB,过点A的双曲线
轴的正半轴上,AC//OB,BC⊥OB,过点A的双曲线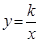 的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
的一支在第一象限交梯形对角线OC于点D,交边BC于点E.
 的取值范围是 ;
的取值范围是 ; ,S△OAC="2" ,求双曲线的解析式.
,S△OAC="2" ,求双曲线的解析式.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
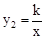 图象的一个交点为M(﹣2,m).
图象的一个交点为M(﹣2,m).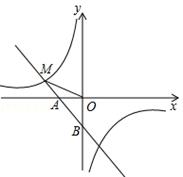
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
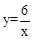 的图象上,则y1,y2,y3的大小关系是【 】
的图象上,则y1,y2,y3的大小关系是【 】| A.y3<y2<y1 | B.y2<y3<y1 | C.y1<y2<y3 | D.y1<y3<y2 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
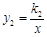 (x>0)的图象交于点A、B,且A、B两点的横坐标分别为2和4.
(x>0)的图象交于点A、B,且A、B两点的横坐标分别为2和4.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com