
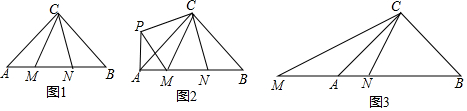
分析 (1)将△BCN绕点C按顺时针方向旋转90°得△ACP,连接MP,根据SAS证得△MCP≌△MCN,得出MP=MN,再根据∠PAM=∠CAP+∠CAB=90°,运用勾股定理得出Rt△APM中,PM2=AM2+AP2,进而得到MN2=AM2+BM2;
(2)将△BCN绕点C按顺时针方向旋转90°得△ACP,连接MP,得出∠PCN=∠ACB=90°,PC=NC,AP=BN,∠CAP=∠B=45°,根据SAS证得△MCP△MCN,进而得出MP=MN,再根据∠PAB=∠CAP+∠CAB=90°,得到∠PAM=90°,在Rt△APM中,根据勾股定理得到PM2=AM2+AP2,进而得出MN2=AM2+BM2..
解答 解:(1)①如图2,将△BCN绕点C按顺时针方向旋转90°得△ACP,连接MP,则
∠BCN=∠ACP,
∵在△ABC中,∠ACB=90°,∠MCN=45°,
∴∠ACM+∠BCN=45°,
∴∠ACP+∠ACM=45°,
∴∠PCM=∠NCM;
②证明:由旋转可得△CAP≌△CBN,
∴AP=BN,PC=NC,∠CAP=∠B=45°,
在△MCP和△MCN中,
$\left\{\begin{array}{l}{PC=NC}\\{∠PCM=∠NCM}\\{CM=CM}\end{array}\right.$,
∴△MCP≌△MCN(SAS),
∴MP=MN,
∵∠PAM=∠CAP+∠CAB=90°,
∴Rt△APM中,PM2=AM2+AP2,
∴MN2=AM2+BM2;
(2)MN2=AM2+BM2,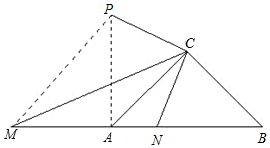
理由:如图,将△BCN绕点C按顺时针方向旋转90°得△ACP,连接MP,则
∠PCN=∠ACB=90°,PC=NC,AP=BN,∠CAP=∠B=45°,
∵∠MCN=45°,
∴∠PCM=90°-45°=45°,
∴∠PCM=∠NCP,
在△MCP和△MCN中,
$\left\{\begin{array}{l}{PC=NC}\\{∠PCM=∠NCM}\\{CM=CM}\end{array}\right.$,
∴△MCP△MCN(SAS),
∴MP=MN,
∵∠PAB=∠CAP+∠CAB=90°,
∴∠PAM=90°,
∴Rt△APM中,PM2=AM2+AP2,
∴MN2=AM2+BM2.
点评 此题属于三角形综合题,主要考查了旋转的性质,等腰直角三角形的性质,勾股定理及全等三角形的判定与性质的综合应用.解题的关键是运用:旋转前、后的图形全等.解题时注意:等腰直角三角形是一种特殊的三角形,具有所有三角形的性质,还具备等腰三角形和直角三角形的所有性质.


科目:初中数学 来源: 题型:填空题
 如图,△ABC、△ADE均为等边三角形,AD平分∠BAC交BC于D,DE交AB于F,则下列结论:①AD⊥BC;②EF=FD; ③BE=BD,其中正确的有①②③(填序号).
如图,△ABC、△ADE均为等边三角形,AD平分∠BAC交BC于D,DE交AB于F,则下列结论:①AD⊥BC;②EF=FD; ③BE=BD,其中正确的有①②③(填序号).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
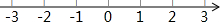 解不等式(组),并把题(2)的解在数轴上表示出来..
解不等式(组),并把题(2)的解在数轴上表示出来..查看答案和解析>>
科目:初中数学 来源: 题型:解答题
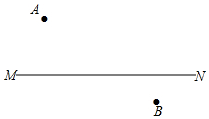 如图,在直线MN的异侧有A、B两点,按要求画图取点,并写出画图的依据.
如图,在直线MN的异侧有A、B两点,按要求画图取点,并写出画图的依据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
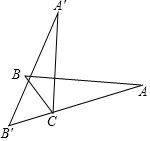 如图,在△ABC中,∠A:∠B:∠ACB=2:5:11,若将△ACB绕点C逆时针旋转,使旋转前后的△A′B′C中的顶点B′在原三角形的边AC的延长线上,求∠BCA′的度数.
如图,在△ABC中,∠A:∠B:∠ACB=2:5:11,若将△ACB绕点C逆时针旋转,使旋转前后的△A′B′C中的顶点B′在原三角形的边AC的延长线上,求∠BCA′的度数.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com