
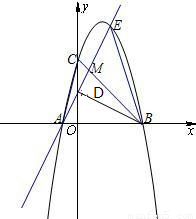
 ,
,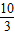 ),AM=
),AM=
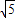 .
.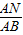 =
=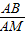 ,即AB2=AM•AN,
,即AB2=AM•AN,
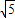 •AN,
•AN,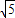 .
.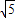 得∠AEB=45°.
得∠AEB=45°.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•衢州模拟)如图,Rt△ABC中,∠C=90°,BC=3,AC=4,点P从点C出发沿C-A-B方向运动到点B,运动速度为1个单位每秒,运动时间为t,当△BCP为等腰三角形时,则t的值为
(2012•衢州模拟)如图,Rt△ABC中,∠C=90°,BC=3,AC=4,点P从点C出发沿C-A-B方向运动到点B,运动速度为1个单位每秒,运动时间为t,当△BCP为等腰三角形时,则t的值为| 27 |
| 5 |
| 13 |
| 2 |
| 27 |
| 5 |
| 13 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2012•衢州模拟)小明为测量门前大树AB的高度,他先从房屋底部D处看树顶A的仰角为60°,之后小明爬上房屋顶部C处看树顶A的俯角为30°,已知小明家的房屋高度为8米,小明的身高忽略不计,求大树AB的高度.
(2012•衢州模拟)小明为测量门前大树AB的高度,他先从房屋底部D处看树顶A的仰角为60°,之后小明爬上房屋顶部C处看树顶A的俯角为30°,已知小明家的房屋高度为8米,小明的身高忽略不计,求大树AB的高度.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com