练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    菱形和矩形一定都具有的性质是( )

    A．对角线相等 B．对角线互相垂直

    C．对角线互相平分且相等 D．对角线互相平分

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：2014-2015学年贵州省黔南州七年级下学期期末数学试卷（解析版） 题型：选择题

    在平面直角坐标系中，点P（﹣2，﹣3）在（ ）

    A．第一象限 B.第二象限 C.第三象限 D.第四象限

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年广东省中山市八年级下学期期末数学试卷（解析版） 题型：填空题

    如图，函数y=ax和y=bx+c的图象相交于点A（1，2），则不等式ax＞bx+c的解集为 ．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年广东省肇庆市封开县八年级下学期数学期末数学试卷（解析版） 题型：解答题

    如图，在正方形ABCD中，E为ED边上的一点，CE=CF,∠FDC=30°，求∠BEF的度数.

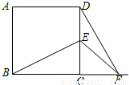
    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年广东省肇庆市封开县八年级下学期数学期末数学试卷（解析版） 题型：填空题

    如图，菱形的两条对角线分别是BD=6和AC=8，则菱形的周长是 .

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年广东省肇庆市封开县八年级下学期数学期末数学试卷（解析版） 题型：选择题

    一次函数y=x-2不经过( )

    A.第一象限 B.第二象限 C.第三象限 D.第四象限

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年山东省青岛市李沧区中考一模数学试卷（解析版） 题型：解答题

    【问题情境】

    张老师给爱好学习的小林和小兰提出这样一个问题：如图①，在△ABC中，AB=AC，点P为边BC上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D、E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．

    小林的证明思路是：如图②，连接AP，由△ABP与△ACP面积之和等于△ABC的面积可以证得：PD+PE=CF．

    小兰的证明思路是：如图②，过点P作PG⊥CF，垂足为G，通过证明四边形PDFG是矩形，

    可得：PD=GF，PE=CG，则PD+PE=CF．

    【变式探究】如图③，当点P在BC延长线上时，其余条件不变，求证：PD﹣PE=CF；

    【结论运用】请运用上述解答中所积累的经验和方法完成下列两题：

    如图④，在平面直角坐标系中有两条直线l1：y=x+3、l2：y=﹣3x+3，若l2上的一点M到l1的距离是1，请运用上述的结论求出点M的坐标．

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年山东省青岛市李沧区中考一模数学试卷（解析版） 题型：选择题

    函数（a≠0）与y=a（x﹣1）（a≠0）在同一坐标系中的大致图象是（ ）

    查看答案和解析>>

    科目：初中数学 来源：2014-2015学年湖北省武汉市九年级元月调考模拟1数学试卷（解析版） 题型：填空题

    已知整数k＜5，若△ABC的边长均满足关于x的方程x2﹣3x+8=0，则△ABC的周长是 ．

    查看答案和解析>>

    同步练习册答案