
分析 首先利用待定系数法求得直线AB的解析式,然后根据CD∥AB即可求得CD的解析式的一次项系数,然后设出CD的解析式,利用判别式求得直线CD的解析式.
解答 解:设直线AB的解析式是y=kx+b,
根据题意得:$\left\{\begin{array}{l}{b=3}\\{-k+b=0}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{b=3}\\{k=3}\end{array}\right.$,
则直线AB的解析式是y=3x+3,
设直线CD的解析式是y=3x+c,
x2-3x-6=3x+c,
即x2-6x-(c+6)=0,
△=36+4(c+6)=0,
解得:c=-15,
则直线CD的解析式是y=3x-15.
点评 本题考查了待定系数法求函数的解析式,理解直线AB和直线CD的解析式之间的关系是关键.


 备战中考寒假系列答案
备战中考寒假系列答案科目:初中数学 来源: 题型:解答题
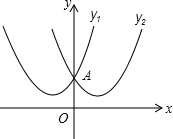 定义感知:我们把顶点关于y轴对称,且交于y轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线y1=x2+2x+2与y2=x2-2x+2是一对“孪生抛物线”,其“共点”为点A.
定义感知:我们把顶点关于y轴对称,且交于y轴上同一点的两条抛物线叫做“孪生抛物线”,该点叫“孪生抛物线”的“共点”.如图所示的抛物线y1=x2+2x+2与y2=x2-2x+2是一对“孪生抛物线”,其“共点”为点A.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{5}{3}$ | B. | -$\sqrt{2}$ | C. | -$\sqrt{3}$ | D. | -$\frac{π}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
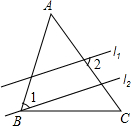 如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=55°,则∠2的大小为( )
如图,直线l1∥l2,且分别与△ABC的两边AB、AC相交,若∠A=50°,∠1=55°,则∠2的大小为( )| A. | 55° | B. | 65° | C. | 75° | D. | 85° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | -$\frac{5}{7}$+$\frac{2}{7}$=1 | B. | 3÷$\frac{5}{4}$×$\frac{4}{5}$=3÷1=3 | C. | -7-2×5=-9×5=-45 | D. | 0-(-22)=22 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com