
 x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).
x2+bx-2与x轴交于A、B两点,与y轴交于C点,且A(一1,0).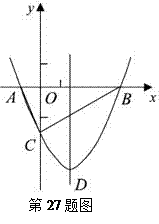
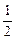 x2 + bx-2上,∴
x2 + bx-2上,∴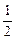 × (-1 )2 + b× (-1) –2 = 0,解得b =
× (-1 )2 + b× (-1) –2 = 0,解得b =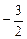
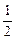 x2-
x2-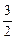 x-2. y=
x-2. y=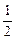 x2-
x2-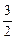 x-2 =
x-2 =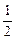 ( x2 -3x- 4 ) =
( x2 -3x- 4 ) =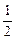 (x-
(x-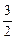 )2-
)2-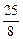 ,
,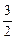 , -
, -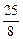 ).
). 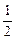 x2-
x2-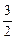 x-2 = 0, ∴x1 =" -1," x2 =" 4, " ∴B (4,0)
x-2 = 0, ∴x1 =" -1," x2 =" 4, " ∴B (4,0)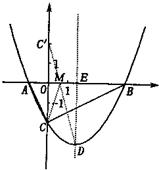
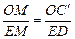
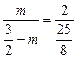 ,∴m =
,∴m =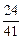 .
.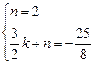 ,解得n =" 2,"
,解得n =" 2," 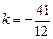 .
.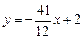 .
. ,
,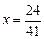 . ∴
. ∴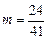 .解析:
.解析:

科目:初中数学 来源: 题型:
 ,求DE的长.
,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:


查看答案和解析>>
科目:初中数学 来源:2011年初中毕业升学考试(浙江台州卷)数学 题型:填空题
(2011贵州安顺,13,4分)已知圆锥的母线长力30,侧面展开后所得扇形的圆心角为120°,则该圆锥的底面半径为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com