
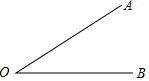
 已知:∠AOB,如图,利用尺规作∠CDE,使∠CDE=∠AOB.
已知:∠AOB,如图,利用尺规作∠CDE,使∠CDE=∠AOB.  轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘,商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:
某商场“五一”期间为进行有奖销售活动,设立了一个可以自由转动的转盘,商场规定:顾客购物100元以上就能获得一次转动转盘的机会,当转盘停止时,指针落在哪一区域就可以获得相应的奖品.下表是此次活动中的一组统计数据:| 转动转盘的次数n | 100 | 200 | 400 | 500 | 800 | 1000 |
| 落在“可乐”区域的次数m | 60 | 122 | 240 | 298 | 476 | 604 |
| 落在“可乐”区域的频率$\frac{m}{n}$ | 0.6 | 0.61 | 0.6 | 0.6 | 0.59 | 0.604 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
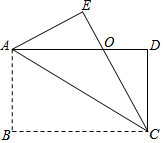 如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.
如图,四边形ABCD是矩形,把矩形沿对角线AC折叠,点B落在点E处,CE与AD相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com