练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    4．计算：$\sqrt{18}$-2sin45°+$\sqrt{（3-π）^{2}}$+（$\frac{1}{3}$）-1．

    分析 直接利用特殊角的三角函数值以及负整数指数幂的性质、算术平方根的性质化简各数进而得出答案．

    解答 解：原式=3$\sqrt{2}$-2×$\frac{\sqrt{2}}{2}$+π-3+3
    =2$\sqrt{2}$+π．

    点评 此题主要考查了实数运算，正确应用负整数指数幂的性质化简是解题关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

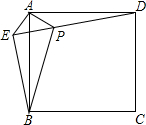    14．如图，点E是正方形ABCD外一点，连接AE，BE和DE，过点A作AE的垂线交DE于P，若AE=AP=1，PB=3，下列结论：
    ①△ADP≌△ABE；
    ②BE⊥DE；
    ③点B到直线AE的距离为$\sqrt{7}$；
    ④S正方形ABCD=8+$\sqrt{14}$，
    其中正确结论的序号是①，②，④．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．在同一坐标系中，一次函数y=ax+b与二次函数y=ax2-b的图象可能是（　　）
    A．B．C．D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    12．下列图形，线段、等边三角形、矩形、圆、正五边形中，既是轴对称图形，又是中心对称图形的个数是（　　）
    A．2B．3C．4D．5

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．计算$\sqrt{12}$+$\frac{6}{\sqrt{3}}$-$\root{3}{27}$的结果是4$\sqrt{3}$-3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

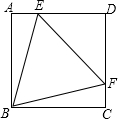    9．如图，正方形ABCD中，点E、F分别在AD、DC上，且△BEF为等边三角形．下列结论：①DE=DF；②∠AEB=75°；③AE+CF=EF；④BE=$\sqrt{2}$DE；⑤△EDF与△BFC的面积比为2：1．其中正确的结论有4个．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

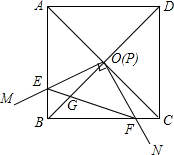    16．如图，边长为1的正方形ABCD的对角线AC、BD相交于点O．有直角∠MPN，使直角顶点P与点O重合，直角边PM、PN分别与OA、OB重合，然后逆时针旋转∠MPN，旋转角为θ（0°＜θ＜90°），PM、PN分别交AB、BC于E、F两点，连接EF交OB于点G，则下列结论中正确的是（1），（2），（3），（5）．
    （1）EF=$\sqrt{2}$OE；（2）S四边形OEBF：S正方形ABCD=1：4；（3）BE+BF=$\sqrt{2}$OA；（4）在旋转过程中，当△BEF与△COF的面积之和最大时，AE=$\frac{3}{4}$；（5）OG•BD=AE2+CF2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    13．下列事件是必然事件的是（　　）
    A．打开电视，正在播放《大国工匠》
    B．袋中只有10个球，且都是红球，任意摸出一个球是红球
    C．5年后数学课代表会考上清华大学
    D．2015年全年由367天

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

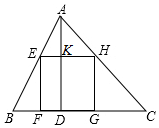    14．若正方形有两个相邻顶点在三角形的同一条边上，其余两个顶点分别在三角形的另两条边上，则正方形称为三角形该边上的内接正方形，△ABC中，设BC=a，AC=b，AB=c，各边上的高分别记为ha，hb，hc，各边上的内接正方形的边长分别记为xa，xb，xc
    （1）模拟探究：如图，正方形EFGH为△ABC的BC边上的内接正方形，求证：$\frac{1}{a}$+$\frac{1}{{h}_{a}}$=$\frac{1}{{x}_{a}}$；
    （2）特殊应用：若∠BAC=90°，xb=xc=2，求$\frac{1}{b}$+$\frac{1}{c}$的值；
    （3）拓展延伸：若△ABC为锐角三角形，b＜c，请判断xb与xc的大小，并说明理由．

    查看答案和解析>>

    同步练习册答案