
【题目】从-2,-1,1,2,3这五个数中随机抽取一数,作为函数y=mx2+2mx+2中的m的值,若能使函数与x轴有两个不同的交点A、B,与y轴的交点为C,且△ABC的面积大于![]() 的概率为:_________
的概率为:_________
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为了了解学生参加体育活动的情况,学校对学生进行随机抽样调查,其中一个问题是“你平均每天参加体育活动的时间是多少”,共有4个选项:A 1.5小时以上;B 1~1.5小时;C 0.5~1小时;D 0.5小时以下.图1、2是根据调查结果绘制的两幅不完整的统计图,请你根据统计图提供的信息,解答以下问题:

(1)本次一共调查了多少名学生?
(2)在图1中将选项B的部分补充完整;
(3)若该校有3000名学生,你估计全校可能有多少名学生平均每天参加体育活动的时间在0.5小时以下.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“五一”假日期间,某网店为了促销,设计了一种抽奖送积分活动,在该网店网页上显示如图所示的圆形转盘,转盘被均等的分成四份,四个扇形上分别标有“谢谢惠顾”、“10分”、“20分”、“40分”字样.参与抽奖的顾客只需用鼠标点击转盘,指针就会在转动的过程中随机的停在某个扇形区域,指针指向扇形上的积分就是顾客获得的奖励积分,凡是在活动期间下单的顾客,均可获得两次抽奖机会,求两次抽奖顾客获得的总积分不低于30分的概率.
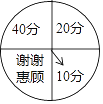
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F
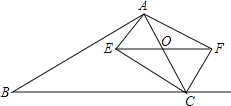
(1)求证:EO=FO;
(2)当点O运动到何处时,四边形CEAF是矩形?请证明你的结论.
(3)在第(2)问的结论下,若AE=3,EC=4,AB=12,BC=13,请直接写出凹四边形ABCE的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰直角![]() 中,
中,![]() ,
,![]() 的角平分线
的角平分线![]() 与
与![]() 的外角平分线
的外角平分线![]() 交于点
交于点![]() ,分别交
,分别交![]() 和
和![]() 的延长线于点
的延长线于点![]() ,
,![]() 过点
过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() 为等腰直角三角形:④
为等腰直角三角形:④![]() .其中正确的结论有__________.
.其中正确的结论有__________.
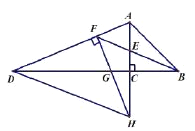
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雅礼集团某学校教学楼需要在规定时间内建造完成,以备迎接新学期的开学,在工程招标时,接到甲、乙两个工程队的投标书如下:(部分信息)


学校后勤处提出两个方案:①由甲工程队独施工;②由乙工程队单独施工;
校团委学生代表小组根据甲、乙两队的投标书测算及工期安排,提出了新的方案:
③若甲乙两队合做4天,余下的工程由乙队单独做也正好如期完成.
试问:(1)学校规定的期限是多少天?
(2)在不耽误工期的前提下,你觉得哪一种施工方案最节省工程款?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三张卡片的正面分别写有数字3、3、4,卡片除数字外完全相同,将它们洗匀后,背面朝上放置在桌面上.
(1)从中任意抽取一张卡片,该卡片上数字是3的概率为_______;
(2)学校将组织歌咏比赛,九年级(1)班只有一个名额,小刚和小芳都想去,于是利用上述三张卡片做游戏决定谁去,游戏规则是:从中任意抽取一张卡片,记下数字后放回,洗匀后再任意抽取一张,将抽取的两张卡片上的数字相加,若和等于6,小刚去;若和等于7,小芳去;和是其他数,游戏重新开始.你认为游戏对双方公平吗?请用画树状图或列表的方法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,M为BC上的点,E是AD的延长线的点,且AE=AM,过E作EF⊥AM垂足为F,EF交DC于点N.
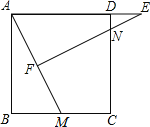
(1)求证:AF=BM;
(2)若AB=12,AF=5,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列两段材料,回答问题:
材料一:点A(x1,y1),B(x2,y2)的中点坐标为(![]() ,
,![]() ).例如,点(1,5),(3,﹣1)的中点坐标为(
).例如,点(1,5),(3,﹣1)的中点坐标为(![]() ,
,![]() ),即(2,2).
),即(2,2).
材料二:如图1,正比例函数l1:y=k1x和l2:y=k2x的图象相互垂直,分别在l1和l2上取点A,B,使得AO=BO.分别过点A,B作x轴的垂线,垂足分别为点C,D.显然,△AOC≌△OBD.设OC=BD=a,AC=OD=b,则A(﹣a,b),B(b,a).于是k1=﹣![]() ,k2=
,k2=![]() ,所以k1k2的值为一个常数.一般地,一次函数y=k1x+b1,y=k2x+b2可分别由正比例函数l1,l2平移得到.
,所以k1k2的值为一个常数.一般地,一次函数y=k1x+b1,y=k2x+b2可分别由正比例函数l1,l2平移得到.
所以,我们经过探索得到的结论是:任意两个一次函数y=k1x+b1,y=k2x+b2的图象相互垂直,则k1k2的值为一个常数.
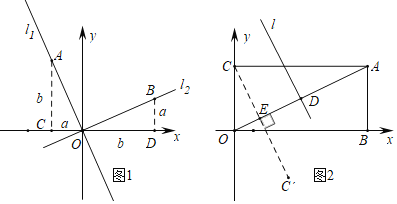
(1)在材料二中,k1k2= (写出这个常数具体的值);
(2)如图2,在矩形OBAC中A(4,2),点D是OA中点,用两段材料的结论,求点D的坐标和OA的垂直平分线l的解析式;
(3)若点C′与点C关于OA对称,用两段材料的结论,求点C′的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com