
 ∠ACB=∠ADC=90°,AC=3,CD=2.当AB的长为$\frac{9\sqrt{5}}{5}$或$\frac{9}{2}$时,这两个直角三角形相似.
∠ACB=∠ADC=90°,AC=3,CD=2.当AB的长为$\frac{9\sqrt{5}}{5}$或$\frac{9}{2}$时,这两个直角三角形相似. 分析 如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例,那么这两个直角三角形相似.在Rt△ABC和Rt△ACD,直角边的对应需分情况讨论.
解答  解:∵AC=3,CD=2,
解:∵AC=3,CD=2,
∴AD=$\sqrt{A{C}^{2}-C{D}^{2}}$=$\sqrt{5}$.要使这两个直角三角形相似,有两种情况:
(1)当Rt△ABC∽Rt△ACD时,有$\frac{AC}{AD}$=$\frac{AB}{AC}$,即$\frac{3}{\sqrt{5}}$=$\frac{AB}{3}$,
则AB=$\frac{9\sqrt{5}}{5}$;
(2)当Rt△ACB∽Rt△CDA时,有 $\frac{AC}{CD}$=$\frac{AB}{AC}$,即:$\frac{3}{2}$=$\frac{AB}{3}$,
则AB=$\frac{9}{2}$.
故当AB的长为$\frac{9\sqrt{5}}{5}$或$\frac{9}{2}$时,这两个直角三角形相似.
故答案是:$\frac{9\sqrt{5}}{5}$或$\frac{9}{2}$.
点评 本题考查相似三角形的判定.识别两三角形相似,除了要掌握定义外,还要注意正确找出两三角形的对应边、对应角,可利用数形结合思想根据图形提供的数据计算对应角的度数、对应边的比.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:解答题
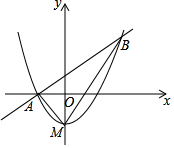 如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.
如图,顶点M在y轴上的抛物线与直线y=x+1相交于A、B两点,且点A在x轴上,点B的横坐标为2,连结AM、BM.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,小明的家D距离大树底部A是9米,一次台风过后,大树在离地面3米的点B处折断,顶端着地处点C在AD上,又知BC恰好等于CD.
如图,小明的家D距离大树底部A是9米,一次台风过后,大树在离地面3米的点B处折断,顶端着地处点C在AD上,又知BC恰好等于CD.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
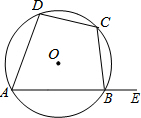 如图,四边形ABCD的四个顶点都在⊙O上,∠ADC=85°,在探究“四点共圆的条件”的活动中,知道∠ADC与∠ABC互补,若∠EBC是ABCD的一个外角,则∠EBC=85°.
如图,四边形ABCD的四个顶点都在⊙O上,∠ADC=85°,在探究“四点共圆的条件”的活动中,知道∠ADC与∠ABC互补,若∠EBC是ABCD的一个外角,则∠EBC=85°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
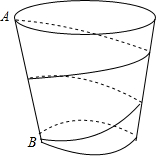 如图,一只杯子的上下底面分别是直径为5cm和7.5cm的圆,母线AB的长为15cm.
如图,一只杯子的上下底面分别是直径为5cm和7.5cm的圆,母线AB的长为15cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 44厘米 | B. | 40厘米 | C. | 36厘米 | D. | 24厘米 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
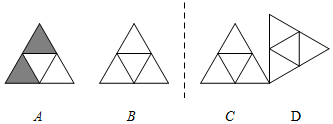
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com