
| 户型 | A | B |
| 成本(万元/套) | 25 | 28 |
| 售价(万元/套) | 30 | 34 |
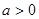 ),且所建的两种住房可全部售出.试问该公司又将如何建房,才能使获得的利润最大。(注:利润=售价-成本)
),且所建的两种住房可全部售出.试问该公司又将如何建房,才能使获得的利润最大。(注:利润=售价-成本)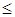 25x+28(80-x )
25x+28(80-x ) 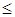 2096
2096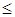 x
x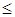 50 经检验,符合题意。
50 经检验,符合题意。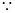 x取整数,
x取整数,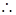 x=48、49、50。
x=48、49、50。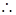 该公司有以下三种建房方案:
该公司有以下三种建房方案: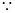 每套A户型获利:30—25=5万元,
每套A户型获利:30—25=5万元,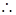 每套B户型获利﹥每套A户型获利,方案一获利最大。
每套B户型获利﹥每套A户型获利,方案一获利最大。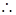 当5+a﹤6,即a﹤1时,方案一获利最大;
当5+a﹤6,即a﹤1时,方案一获利最大;

科目:初中数学 来源:不详 题型:解答题
 的自然数解,求 可能表示的数字。
的自然数解,求 可能表示的数字。查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.2x<-8的解集是x<-4。 | B.x<5的正整数解有无穷个。 |
| C.-15是2x<-8的解。 | D.x>-3的非负整数解有无穷个。 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com