
有六张完全相同的卡片,分A、B两组,每组三张,在A组的卡片上分别画上“√、×、√”,B组的卡片上分别画上“√、×、×”,如图1所示。
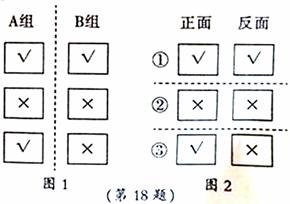
(1)若将卡片无标记的一面朝上摆在桌上,再发布从两组卡片中随机各抽取一张,求两张卡片上标记都是√的概率(请用树形图法或列表法求解)
(2)若把A、B两组卡片无标记的一面对应粘贴在一起得到3张卡片,其正反面标记如图2所示,将卡片正面朝上摆放在桌上,并用瓶盖盖住标记。
①若随机揭开其中一个盖子,看到的标记是√的概率是多少
②若揭开盖子,看到的卡片正面标记是√后,猜想它的反面也是√,求猜对的概率。
(1)解法一:
根据题意,可画出如下树形图:
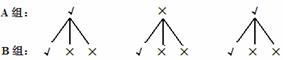
从树形图可以看出,所有可能结果共有9种,且每种结果出现的可能性都相等,其中两张卡片上标记都是“√”的结果有2种。
∴P(两张都是“√”)=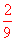 .
.
解法二:
根据题意,可列表如下:

从上表中可以看出,所有可能结果共有9种,且每种结果出现的可能性都相等,其中两张卡片上标记都是“√”的结果有2种。
(2)
①∵根据题意,三张卡片正面的标记有三种可能,分别为“√”、“×”、“√”,
∴随机揭开其中一个盖子,看到的标记是“√”的概率为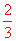 .
.
②∵正面标记为为“√”的卡片,它的反面标记只有两种情况,分别为“√”和“×”,
∴猜对反面也是“√”的概率为P=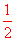 .
.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
提出问题:
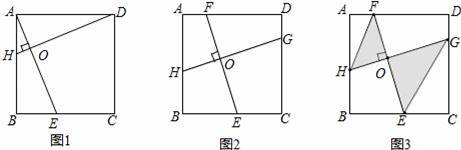
(1)如图1,在正方形ABCD中,点E,H分别在BC,AB上,若AE⊥DH于点O,求证:AE=DH;
类比探究:
(2)如图2,在正方形ABCD中,点H,E,G,F分别在AB,BC,CD,DA上,若EF⊥HG于点O,探究线段EF与HG的数量关系,并说明理由;
综合运用:
(3)在(2)问条件下,HF∥GE,如图3所示,已知BE=EC=2,EO=2FO,求图中阴影部分的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
小明同学用配方法推导关于x的一元二次方程ax2+ bx + c = 0的求根公式时,对于b2-4ac>0的情况,他是这样做的:
小明的解法从第 步开始出现错误;这一步的运算依据应是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
在Rt△ABC中,∠A=90°,有一个锐角为60°,BC=6.若P在直线AC上(不与点A,C重合),且∠ABP=30°,则CP的长为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
某电子商投产一种新型电子产品,每件制造成本为18元,试销过程发现,每月销量
y(万件)与销售单价x(元)之间的关系可以近似地看作一次函数y=-2x+100.
(1)写出每月的利润z(万元)与销售单价x(元)之间函数解析式;
(2)当销售单价为多少元时,厂商每月能够获得最大利润?最大利润是多少?
(3)根据相关部门规定,这种电子产品的销售单价不得高于32元.如果厂商要获得每月不低于350万元的利润,那么制造这种产品每月的最低制造成本需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
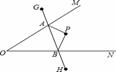
如图,∠MON内有一点P,P点关于OM的轴对称点是G,P点关于ON的轴对称点是H, GH分别交OM、ON于A、B点,若GH的长为10cm,求△PAB的周长为( )
A.5cm B.10cm C.20cm D.15cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com