使得m2+m+7是完全平方数的所有整数m的积是 .
【答案】
分析:将m
2+m+7表示为k
2的形式,然后转化可得出(2m+2k+1)(2m-2k+1)=-27,从而讨论可得出m的值,从而得到所有整数m的积.
解答:解:设m
2+m+7=k
2,
所以m
2+m+

+
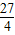
=k
2,
所以(m+
 )2
)2+
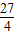
=k
2,
所以 (m+
 )2
)2-k
2=-
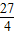
,
所以(m+

+k)(m+

-k)=-
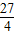
,
所以(2m+2k+1)(2m-2k+1)=-27
因为k≥0(因为k
2为完全平方数),且m与k都为整数,
所以①2m+2k+1=27,2m-2k+1=-1,解得:m=6,k=7;
②2m+2k+1=9,2m-2k+1=-3,解得:m=1,k=3;
③2m+2k+1=3,2m-2k+1=-9,解得:m=-2,k=3;
④2m+2k+1=1,2m-2k+1=-27,解得:m=-7,k=7.
所以所有m的积为6×1×(-2)×(-7)=84.
故答案为:84.
点评:本题考查完全平方数的知识,难度较大,关键是将m
2+m+7表示为k
2的形式,得到(2m+2k+1)(2m-2k+1)=-27,同时也要掌握讨论法的运用.

 +
+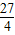 =k2,
=k2, )2+
)2+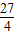 =k2,
=k2, )2-k2=-
)2-k2=-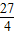 ,
, +k)(m+
+k)(m+ -k)=-
-k)=-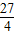 ,
,

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案