练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

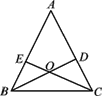
    如图，△ABC中，D，E分别是AC，AB上的点，BD与CE交于点O.给出下列三个条件：①∠EBO＝∠DCO；②∠BEO＝∠CDO；③BE＝CD.上述三个条件中，哪两个条件可判定△ABC是等腰三角形(用序号写出一种情形)：_______．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源：人教版九年级数学下册第29章投影与视图单元测试卷 题型：单选题

    在阳光下摆弄一个矩形，它的影子不可能是（ ）

    A. 线段 B. 矩形 C. 等腰梯形 D. 平行四边形

    查看答案和解析>>

    科目：初中数学 来源：2018年珠海市毕业生学业考试（模拟） 题型：填空题

    若2x+y=2，则4x+1+2y的值是_______．

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级数学上册 13.3.2 等边三角形专题训练试卷 题型：单选题

    一个等腰三角形的两边长分别是4和9，则它的周长是 ( )

    A. 22 B. 17 C. 13 D. 17或22

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级数学上册 13.3.2 等边三角形专题训练试卷 题型：单选题

    如图，在△ABC中，AB=AD=DC，∠B=70°，则∠C的度数为（　　）

    A. 35° B. 40° C. 45° D. 50°

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级数学上册 13.3.2 等边三角形专题训练试卷 题型：填空题

    等腰三角形一个角为70°，则它的底角的度数是_____．

    查看答案和解析>>

    科目：初中数学 来源：人教版八年级数学上册 13.3.2 等边三角形专题训练试卷 题型：填空题

    在等腰三角形ABC中，∠A=120°，则∠C= ．

    查看答案和解析>>

    科目：初中数学 来源：人教版七年级数学上册第三章一元一次方程章末提升练习题 题型：单选题

    同学们，足球是世界上第一大运动，你热爱足球运动吗？已知在足球比赛中，胜一场得3分，平一场得1分，负一场得0分，一队共踢了30场比赛，负了9场，共得47分，那么这个队胜了（　　）

    A. 10场 B. 11场 C. 12场 D. 13场

    查看答案和解析>>

    科目：初中数学 来源：河北省2019届九年级上学期期中考试数学试卷 题型：解答题

    请阅读下列材料，并完成相应的任务：

    阿基米德折弦定理

    阿拉伯Al-Biruni（973年~1050年）的译文中保存了阿基米德折弦定理的内容，苏联在1964年根据Al-Biruni译本出版了俄文版《阿基米德全集》，第一题就是阿基米德的折弦定理．

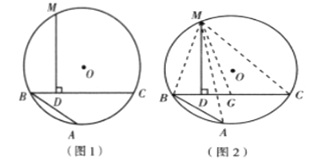
    阿基米德折弦定理：如图1，AB和BC是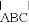的两条弦（即折线ABC是圆的一条折弦），BC>AB，M是的中点，则从M向BC所作垂线的垂足D是折弦ABC的中点，即CD=AB+BD．

    下面是运用“截长法”证明CD=AB+BD的部分证明过程．

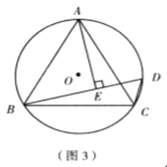
    证明：如图，在CB上截取CG=AB，连接MA，MB，MC和MG．∵M是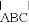的中点， ∴MA=MC ．．．

    任务：（1）请按照上面的证明思路，写出该证明的剩余部分；

    （2）填空：如图（3），已知等边△ABC内接于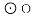，AB=2，D为圆上一点，∠ABD=45°，AE⊥BD与点E，则△BDC的周长是 ．

    查看答案和解析>>

    同步练习册答案