
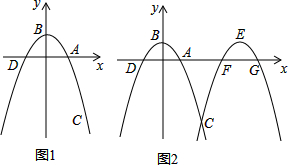
���� ��1������������y1=-x2+a��x�ύ��A��D���㣬��y�ύ�ڵ�B����C��2��-3����������y1��ͼ���ϣ��������������y1�ĺ�������ʽ����B�����ꣻ
��2���ٸ���������y1��x������ƽ�ƺ��������y2����������y2��ͼ�����C������ΪE�����Եõ�������y2�ĺ�������ʽ����E�����ꣻ
���������A��B��C��D��E��F��G��������꣬Ȼ�ɵõ��ܹ��ɵ���ֱ�������εĸ�����ͨ���������˵���ļ����������ǵ���ֱ�������Σ�
��� �⣺��1���ѵ�C��2��-3������y1=-x2+a����
-3=-22+a��
��ã�a=1��
��y1=-x2+1��
��x=0ʱ��y1=1��
����B��������0��1����
��2����������y2�ĺ�������ʽΪ��${y}_{2}=-��x-4��^{2}+1$����E������Ϊ��4��1����
���ɣ���${y}_{2}=-��x+b��^{2}+1$��
�ߵ�C��2��-3����������y2��ͼ���ϣ�
��-3=-��2+b��2+1��
��ã�b=-4��
��${y}_{2}=-��x-4��^{2}+1$��
���E��������4��1����
��3����y1=0����y1=-x2+1����x=-1��x=1����x=0����y1=-x2+1����y1=1��
���D��-1��0������A��1��0������B��0��1����
��y2=0����${y}_{2}=-��x-4��^{2}+1$����x=3��x=5����x=4����${y}_{2}=-��x-4��^{2}+1$����y2=1��
���F��3��0����G��5��0����E��4��1����
��BD=$\sqrt{2}$��AB=$\sqrt{2}$��AD=2��
��$��\sqrt{2}��^{2}+��{\sqrt{2}��}^{2}=4={2}^{2}$��
���ABD�ǵ���ֱ�������Σ�
��EF=$\sqrt{2}$��EG=$\sqrt{2}$��FG=2��
����$��\sqrt{2}��^{2}+��{\sqrt{2}��}^{2}=4={2}^{2}$��
���EFG�ǵ���ֱ�������Σ�
��A��1��0����C��2��-3����E��4��1����
��AC=$\sqrt{��2-1��^{2}+��-3-0��^{2}}=\sqrt{10}$��AE=$\sqrt{��4-1��^{2}+��1-0��^{2}}=\sqrt{10}$��CE=$\sqrt{��2-4��^{2}+��-3-1��^{2}}=\sqrt{20}$��
��$��\sqrt{10}��^{2}+��\sqrt{10}��^{2}=��{\sqrt{20}��}^{2}$��
���ACE�ǵ���ֱ�������Σ�
�ߵ�BΪ��0��1����CΪ��2��-3������F��3��0����
��BC=$\sqrt{��2-0��^{2}+��{-3-1��}^{2}}=\sqrt{20}$��BF=$\sqrt{��3-0��^{2}+��{0-1��}^{2}}=\sqrt{10}$��CF=$\sqrt{��2-3��^{2}+��-3-0��^{2}}=\sqrt{10}$��
��$��\sqrt{10}��^{2}+��\sqrt{10}��^{2}=��{\sqrt{20}��}^{2}$��
���BCF�ǵ���ֱ�������Σ�
�ߵ�DΪ��-1��0����CΪ��2��-3����GΪ��5��0����
��DC=$\sqrt{[2-��-1��]^{2}+[��-3��-0]^{2}}=\sqrt{18}$��DG=$\sqrt{��-1-5��^{2}+��0-0��^{2}}=\sqrt{36}$��CG=$\sqrt{��2-5��^{2}+��-3-0��^{2}}=\sqrt{18}$��
��$��\sqrt{18}��^{2}+��\sqrt{18}��^{2}=��\sqrt{36}��^{2}$��
���CDG�ǵ���ֱ�������Σ�
�ʴ�Ϊ��5����ABD����EFG����BFC����ACE����CDG��
���� ���⿼����κ����ۺ��⡢�����ľ��롢����ֱ�������ε��ж������ɶ������涨��������Ĺؼ�����ȷ���⣬�ҳ�����������Ҫ���������������ν�ϵ�˼�������⣮


 һ��һ����ʱ���ϵ�д�
һ��һ����ʱ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | 2$\sqrt{3}$ | C�� | -$\frac{1}{2}$ | D�� | -2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
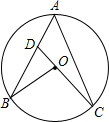 ��ͼ����A��B��C�ڡ�O�ϣ�CO���ӳ��߽�AB�ڵ�D��BD=BO����A=50�㣬���B�Ķ���Ϊ��������
��ͼ����A��B��C�ڡ�O�ϣ�CO���ӳ��߽�AB�ڵ�D��BD=BO����A=50�㣬���B�Ķ���Ϊ��������| A�� | 15�� | B�� | 20�� | C�� | 25�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ1���ֱ���ֱ������������Ϊ���������ȱ������Σ�����ֱ�ΪS1��S2��S3����ͼ2���ֱ���ֱ����������������ΪԲ�ģ����߳�Ϊ�뾶������Բ�Ľ���ȵ����Σ�����ֱ�ΪS4��S5��S6������S1=16��S2=45��S5=11��S6=14����S3+S4=��������
��ͼ1���ֱ���ֱ������������Ϊ���������ȱ������Σ�����ֱ�ΪS1��S2��S3����ͼ2���ֱ���ֱ����������������ΪԲ�ģ����߳�Ϊ�뾶������Բ�Ľ���ȵ����Σ�����ֱ�ΪS4��S5��S6������S1=16��S2=45��S5=11��S6=14����S3+S4=��������| A�� | 86 | B�� | 64 | C�� | 54 | D�� | 48 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��1000�������������һ������ | B�� | 1000���������������� | ||
| C�� | ÿλ��������ѧ�ɼ��Ǹ��� | D�� | ��9��������������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��$-\frac{3}{2}$ | B�� | x��-$\frac{3}{2}$ | C�� | x��-$\frac{2}{3}$ | D�� | x��-$\frac{2}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
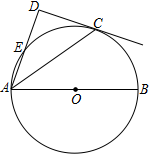 ��ͼ����C����ABΪֱ���ġ�O�ϣ�AD�����C�����ߴ�ֱ������Ϊ��D��AD����O�ڵ�E��
��ͼ����C����ABΪֱ���ġ�O�ϣ�AD�����C�����ߴ�ֱ������Ϊ��D��AD����O�ڵ�E���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����ƽ��ֱ������ϵ�У���M��x�������ڵ�A��8��0������y��ֱ��ڵ�B��0��4���͵�C��0��16������Բ��M������ԭ��O�ľ����ǣ�������
��ͼ����ƽ��ֱ������ϵ�У���M��x�������ڵ�A��8��0������y��ֱ��ڵ�B��0��4���͵�C��0��16������Բ��M������ԭ��O�ľ����ǣ�������| A�� | 10 | B�� | 8$\sqrt{2}$ | C�� | 4$\sqrt{13}$ | D�� | 2$\sqrt{41}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com